题目内容
11.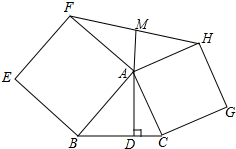 如图,分别以△ABC的边AB,AC为一边在三角形外作正方形ABEF和ACGH,M为FH上的中点,求证:MA⊥BC.
如图,分别以△ABC的边AB,AC为一边在三角形外作正方形ABEF和ACGH,M为FH上的中点,求证:MA⊥BC.
分析 延长AM到N使MN=AM,如图,先证明△AMF≌△NMB得到∠MAF=∠N,AF=NH,再证明∠BAC=∠AHN,接着证明△ABC≌△HNA得到∠ACB=∠HAN,然后证明∠ADC=90°,从而得到结论.
解答 证明:延长AM到N使MN=AM,如图,
∵M为FH上的中点,
∴FM=HM,
在△AMF和△NMB中,
$\left\{\begin{array}{l}{AM=NM}\\{∠AMF=∠NMH}\\{FM=HM}\end{array}\right.$,
∴△AMF≌△NMB,
∴∠MAF=∠N,AF=NH,
∵四边形ABEF和四边形ACGH为正方形,
∴AB=AF,AC=AH,∠BAF=∠CAH=90°,
∴∠FAH+∠BAC=180°,HN=AB,
∴∠N+∠NAH+∠BAC=180°,
∵∠N+∠NAH+∠AHN=180°,
∴∠BAC=∠AHN,
在△ABC和△HNA中,
$\left\{\begin{array}{l}{AB=HN}\\{∠BAC=∠BHA}\\{AC=HA}\end{array}\right.$,
∴△ABC≌△HNA,
∴∠ACB=∠HAN,
∵∠HAN+∠CAD=90°,
∴∠ACD+∠CAD=90°,
∴∠ADC=90°,
∴AD⊥BC.
点评 本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.解决本题的关键是构造△AHN与△CBA全等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13. 如图,△ABC是等边三角形,CB=BD,连接AD,∠ACD=110°,则∠BAD的度数为( )
如图,△ABC是等边三角形,CB=BD,连接AD,∠ACD=110°,则∠BAD的度数为( )
 如图,△ABC是等边三角形,CB=BD,连接AD,∠ACD=110°,则∠BAD的度数为( )
如图,△ABC是等边三角形,CB=BD,连接AD,∠ACD=110°,则∠BAD的度数为( )| A. | 10° | B. | 15° | C. | 20° | D. | 25° |
1.下列数组不能构成直角三角形三边长的是( )
| A. | 3,4,5 | B. | 5,12,13 | C. | 1,$\sqrt{2}$,$\sqrt{3}$ | D. | 2,3,4 |
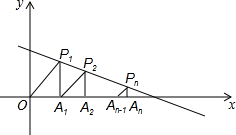 如图所示,在函数y=-$\frac{1}{3}$x+$\frac{4}{3}$(x>0)的图象上,△P1OA,△P2A1A2,△P2A2A3,…,△PnAn-1An都是等腰直角三角形,且直角边OA1,A1A2,…,An-1An都在x轴上,则An的坐标为Pn[1+$\frac{3}{4}$+$\frac{9}{16}$+…($\frac{3}{4}$)n-1,($\frac{3}{4}$)n-1].
如图所示,在函数y=-$\frac{1}{3}$x+$\frac{4}{3}$(x>0)的图象上,△P1OA,△P2A1A2,△P2A2A3,…,△PnAn-1An都是等腰直角三角形,且直角边OA1,A1A2,…,An-1An都在x轴上,则An的坐标为Pn[1+$\frac{3}{4}$+$\frac{9}{16}$+…($\frac{3}{4}$)n-1,($\frac{3}{4}$)n-1].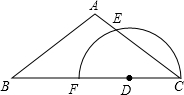 已知:如图,在△ABC中,D是边BC上一点,以点D为圆心,CD为半径作半圆,分别与边AC、BC相交于点E和点F.如果AB=AC=5,cosB=$\frac{4}{5}$,AE=1.求:
已知:如图,在△ABC中,D是边BC上一点,以点D为圆心,CD为半径作半圆,分别与边AC、BC相交于点E和点F.如果AB=AC=5,cosB=$\frac{4}{5}$,AE=1.求:
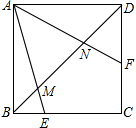 如图,正方形ABCD中,点E、F分别是BC、CD边上的点,且∠EAF=45°,对角线BD交AE于点M,交AF于点N.若AB=4$\sqrt{2}$,BM=2,则MN的长为$\frac{10}{3}$.
如图,正方形ABCD中,点E、F分别是BC、CD边上的点,且∠EAF=45°,对角线BD交AE于点M,交AF于点N.若AB=4$\sqrt{2}$,BM=2,则MN的长为$\frac{10}{3}$.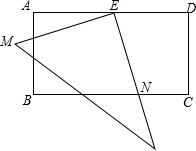 在长方形ABCD中,AD=2AB,E是AD的中点,一块三角板的直角顶点与点E重合,将三角板绕点E按顺时针方向旋转,当三角板的两直角边分别与AB、BC分别相交于点M,N时,观察或测量BM与CN的长度,你能得到什么结论?并证明你的结论.
在长方形ABCD中,AD=2AB,E是AD的中点,一块三角板的直角顶点与点E重合,将三角板绕点E按顺时针方向旋转,当三角板的两直角边分别与AB、BC分别相交于点M,N时,观察或测量BM与CN的长度,你能得到什么结论?并证明你的结论.