题目内容
9．在△ABC中，若a=$\sqrt{2n}$，b=$\sqrt{{n}^{2}+1}$，c=n-1，则△ABC的形状是（ ）| A． | 锐角三角形 | B． | 钝角三角形 | C． | 等腰三角形 | D． | 直角三角形 |
分析 根据勾股定理的逆定理：如果三角形有两边的平方和等于第三边的平方，那么这个是直角三角形判定则可．如果有这种关系，这个就是直角三角形．
解答 解：∵（n-1）2+（$\sqrt{2n}$）2=（$\sqrt{{n}^{2}+1}$）2，
∴三角形为直角三角形．
故选D．
点评 本题利用了勾股定理的逆定理判定直角三角形，即已知△ABC的三边满足a2+b2=c2，则△ABC是直角三角形．
练习册系列答案
小学夺冠AB卷系列答案
ABC考王全优卷系列答案
相关题目
17．如表是某校七～九年级某月课外兴趣小组（分文艺小组和科技小组）活动时间统计表，其中各年级同一兴趣小组每次活动时间相同．
（Ⅰ）请你完成以下的分析，求出a，b的值：
观察表格，七、八年级科技小组活动次数相同，文艺小组活动次数相差1次，活动总时间相差2h，由此可知文艺小组每次活动时间为2h，进而可知科技小组每次活动时间为1.5h；
依题意可得a与b的关系式为2a+1.5b=7，因为a与b是自然数，所以a=2，b=2；
（Ⅱ）若学校重新规定：九年级每月课外兴趣小组活动总次数为8次，在文艺小组与科技小组每次活动时间保持不变的情况下，求出九年级每月课外兴趣小组活动总时间y（h）与文艺小组活动次数x（次）之间的函数关系式（其中规定x为大于1且小于8的自然数）．
| 课外小组活动总时间h | 文艺小组活动次数 | 科技小组活动次数 | |
| 七年级 | 12.5 | 4 | 3 |
| 八年级 | 10.5 | 3 | 3 |
| 九年级 | 7 | a | b |
观察表格，七、八年级科技小组活动次数相同，文艺小组活动次数相差1次，活动总时间相差2h，由此可知文艺小组每次活动时间为2h，进而可知科技小组每次活动时间为1.5h；
依题意可得a与b的关系式为2a+1.5b=7，因为a与b是自然数，所以a=2，b=2；
（Ⅱ）若学校重新规定：九年级每月课外兴趣小组活动总次数为8次，在文艺小组与科技小组每次活动时间保持不变的情况下，求出九年级每月课外兴趣小组活动总时间y（h）与文艺小组活动次数x（次）之间的函数关系式（其中规定x为大于1且小于8的自然数）．
如图是某建筑物的屋顶架，其中AB=8m，D是AB的中点，BC，DE都垂直于AC．如果∠ABC=60°，那么BC，DE，CD各是多少米？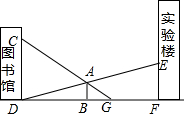
某中学的图书馆与实验楼中间有一地标牌AB，小鸣和小夕两位同学分别在图书馆和实验楼的C、E两点处观测地标牌的顶端A，他们的视线如图所示，小鸣从点C处可以看到地面上距离实验楼底部10米远的点G处，小夕从点E恰好可以看到图书馆的底部D处，已知图中的所有点均在同一平面内，CD⊥DF，AB⊥DF，EF⊥DF，CD=6米，EF=3米，DF=25米，请你根据以上数据，求该地标牌的高度AB及它与图书馆之间的距离BD（结果精确到0.1米）．