题目内容
19. 如图是一个汉字“互”字,其中,GH∥EF,∠1=∠2,∠MEF=∠GHN.求证:
如图是一个汉字“互”字,其中,GH∥EF,∠1=∠2,∠MEF=∠GHN.求证:(1)∠MGH=∠GHN;
(2)AB∥CD.
分析 (1)由GH∥EF,根据两直线平行同位角相等可得:∠MEF=∠MGH,然后由∠MEF=∠GHN,根据等量代换可得:∠MGH=∠GHN;
(2)延长ME交CD于P点,然后由∠MGH=∠GHN,根据内错角相等两直线平行,可得:ME∥HN,进而根据两直线平行同位角相等,可得:∠3=∠2,然后由∠1=∠2,根据等量代换可得:∠1=∠3,然后根据内错角相等两直线平行可得:AB∥CD.
解答 证明:(1)∵GH∥EF
∴∠MEF=∠MGH
又∵∠MEF=∠GHN
∴∠MGH=∠GHN
(2)延长ME交CD于P点,
∵∠MGH=∠GHN
∴ME∥HN
∴∠3=∠2
∵∠1=∠2
∴∠1=∠3
∴AB∥CD.
点评 此题考查了平行线的性质与判定,熟记同位角相等?两直线平行,内错角相等?两直线平行,同旁内角互补?两直线平行是解题的关键.

练习册系列答案
相关题目
10. 把一块直尺与一块三角板如图放置,若∠1=40°,则∠2的度数为( )
把一块直尺与一块三角板如图放置,若∠1=40°,则∠2的度数为( )
 把一块直尺与一块三角板如图放置,若∠1=40°,则∠2的度数为( )
把一块直尺与一块三角板如图放置,若∠1=40°,则∠2的度数为( )| A. | 130° | B. | 140° | C. | 120° | D. | 125° |
4.下列各图中,∠1与∠2是内错角的是( )
| A. | 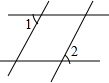 | B. | 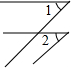 | C. | 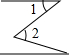 | D. | 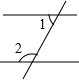 |
 如图,?ABCD中,AE⊥BC于E,AF⊥CD于F,∠BAD=135°,则∠EAF=45°.
如图,?ABCD中,AE⊥BC于E,AF⊥CD于F,∠BAD=135°,则∠EAF=45°.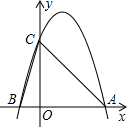 如图所示,二次函数y=-2x2+4x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
如图所示,二次函数y=-2x2+4x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.