题目内容
1．
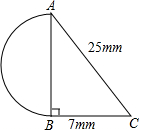某零件截面的形状及有关尺寸如图，它是由一个直角三角形和一个半圆组成，求出这个零件的截面积（结果保留π）．
分析 先根据勾股定理求出AB的长，再由圆和直角三角形的面积公式即可得出结论．
解答 解：∵△ABC是直角三角形，
∴AB=$\sqrt{A{C}^{2}-B{C}^{2}}$=$\sqrt{2{5}^{2}-{7}^{2}}$=24，
∴这个零件的截面积=S半圆+S△ABC=$\frac{1}{2}$π×122+$\frac{1}{2}$×7×24=72π+84．
点评 本题考查的是勾股定理的应用、扇形及三角形的面积公式等知识，难度适中．
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
如图，直线AB与CD相交于点O，∠AOC=$\frac{1}{3}$∠AOD，求∠BOD的度数．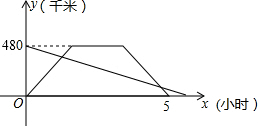
一辆动车和一辆普快分别从A、B两地同时出发相向而行，动车到达B地停留1小时后原速返回A地，结果比普快早1小时到达A地，它们离A地的路程随时间变化的图象如图所示，则下列结论中正确的个数是（ ）
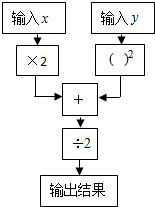求代数式的值：