题目内容
10．如图（1），是一个长为2a宽为2b（a＞b）的矩形，用剪刀沿矩形的两条对角轴剪开，把它分成四个全等的小矩形，然后按图（2）拼成一个新的正方形，求中间空白部分的面积（用含a、b的式子表示）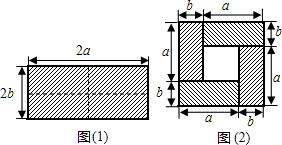
分析 先求出正方形的边长，根据空白部分的面积=正方形的面积-矩形的面积即可得出答案．
解答 解：由题意可得，正方形的边长为（a+b），故正方形的面积为（a+b）2，
∵原矩形的面积为4ab，
∴空白部分的面积=正方形的面积-矩形的面积=（a+b）2-4ab=（a-b）2．
点评 本题考查的是完全平方公式的几何背景，正确找出空白部分的面积与正方形的面积、矩形的面积的关系是解题的关键．
练习册系列答案
习题精选系列答案
相关题目
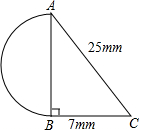某零件截面的形状及有关尺寸如图，它是由一个直角三角形和一个半圆组成，求出这个零件的截面积（结果保留π）．
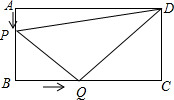如图所示，在长方形ABCD中，AB=6厘米，BC=12厘米，点P沿AB边从点A开始向点B以1厘米/秒的速度移动，点Q沿BC从点B开始向点C以2厘米/秒的速度移动，如果P、Q同时出发，用t（秒）表示移动的时间（0≤t≤6）．
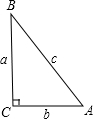已知：如图，直角三角形BCA中，∠BCA=90°，BC=a，CA=b，AB=c，请你用两种方法证明：a2+b2=c2．
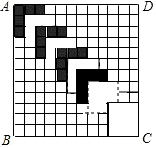如图，正方形ABCD的边长为12，划分成12×12个小正方形格．将边长为n（n为整数，且2≤n≤11）的黑白两色正方形纸片按图中的方式黑白相间地摆放，第一张n×n的纸片正好盖住正方形ABCD左上角的n×n个小正方形格，第二张纸片盖住第一张纸片的部分恰好为（n-1）×（n-1）的正方形．如此摆放下去，最后直到纸片盖住正方形ABCD的右下角为止．请你认真观察思考后回答下列问题：
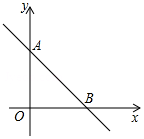如图，直线y=$\frac{\sqrt{3}}{3}x$+1和x轴、y轴分别交于点A、B．若以线段AB为边作等边三角形ABC，则点C的坐标是（$\sqrt{3}$，2）或（0，-1）．