题目内容

7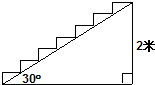．如图，在高为2m，坡角为30°的楼梯表面铺地毯，地毯的长度至少需要（　　）
A．2（$\sqrt{3}$+1）mB．4mC．（$\sqrt{3}$+2）mD．2（$\sqrt{3}$+3）m

分析 由题意得，地毯的总长度至少为（AC+BC）．在△ABC中已知一边和一个锐角，满足解直角三角形的条件，可求出AC的长，进而求得地毯的长度．

解答 解：由题意得：地毯的竖直的线段加起来等于BC，水平的线段相加正好等于AC，
即地毯的总长度至少为（AC+BC），
在Rt△ABC中，∠A=30°，BC=2m，∠C=90°．
∵tanA=$\frac{BC}{AC}$，
∴AC=BC÷tan30°=2$\sqrt{3}$．
∴AC+BC=2$\sqrt{3}$+2．
故选A．

点评 本题考查了解直角三角形的应用，解题的关键是明白每个台阶的两条直角边的和是直角△ABC的直角边的和．

练习册系列答案
相关题目
17．已知a＜0，b＞0，且a2+5a=$\frac{1}{b}$+$\frac{5}{\sqrt{b}}$=1，则代数式$\frac{{a}^{3}b\sqrt{b}+1}{b\sqrt{b}}$的值为-140．
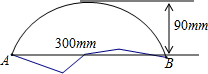18．一支考古队发现一个残破的古代圆盘碎片，如图所示，考古家测量了弦AB=300mm，圆弧的高为90mm，于是得到了古圆盘的半径，从而确定了它的圆心，终于使这个古物得以复原，请问你知道考古家怎样得到它的半径吗？
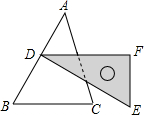15．如图，含30°角的直角三角尺DEF放置在△ABC上，30°角的顶点D在边AB上，DE⊥AB，且BC∥DF．若∠A=50°，则∠C的度数为70°．
2．已知一直角三角形的木版，三边的平方和为1800cm2，则斜边长为（　　）
A．80mB．30mC．90mD．120m
12．计算
（-16）+8=-8；    
（-72）-（+63）=-135；
（-$\frac{1}{2}$）×4=-2；  
-$\frac{2}{3}$×（-6）=4．
19．已知∠AOB=50°，∠BOC=30°，求∠AOC的度数．
16．$\frac{1}{1×2}=1-\frac{1}{2}$，$\frac{1}{2×3}=\frac{1}{2}-\frac{1}{3}$，$\frac{1}{3×4}=\frac{1}{3}-\frac{1}{4}$．
将以上三个等式两边分别相加得：$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$=1-$\frac{1}{4}$=$\frac{3}{4}$．
（1）猜想并写出：$\frac{1}{n（n+1）}$=$\frac{1}{n}$-$\frac{1}{n+1}$；
（2）直接写出下列各式的计算结果：
①$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2006×2007}$=$\frac{2006}{2007}$；
②$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{n（n+1）}$=$\frac{n}{n+1}$；
（3）探究并计算：
①$\frac{1}{2×4}$+$\frac{1}{4×6}$+$\frac{1}{6×8}$+…+$\frac{1}{2006×2008}$
②$\frac{1}{1×4}$+$\frac{1}{4×7}$+$\frac{1}{7×10}$+$\frac{1}{10×13}$+$\frac{1}{13×16}$+$\frac{1}{16×19}$．
17．$\frac{3}{5}$的相反数与-$\frac{2}{5}$的绝对值的差是-1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网