题目内容
7.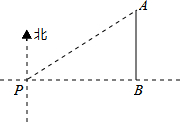 如图,一艘海轮位于灯塔P的北偏东55°方向,距离灯塔2海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向,海轮航行的距离AB长是( )
如图,一艘海轮位于灯塔P的北偏东55°方向,距离灯塔2海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向,海轮航行的距离AB长是( )| A. | 2海里 | B. | 2sin55°海里 | C. | 2cos55°海里 | D. | 2tan55°海里 |
分析 首先由方向角的定义及已知条件得出∠NPA=55°,AP=2海里,∠ABP=90°,再由AB∥NP,根据平行线的性质得出∠A=∠NPA=55°.然后解Rt△ABP,得出AB=AP•cos∠A=2cos55°海里.
解答  解:如图,由题意可知∠NPA=55°,AP=2海里,∠ABP=90°.
解:如图,由题意可知∠NPA=55°,AP=2海里,∠ABP=90°.
∵AB∥NP,
∴∠A=∠NPA=55°.
在Rt△ABP中,∵∠ABP=90°,∠A=55°,AP=2海里,
∴AB=AP•cos∠A=2cos55°海里.
故选C.
点评 本题考查了解直角三角形的应用-方向角问题,平行线的性质,三角函数的定义,正确理解方向角的定义是解题的关键.

练习册系列答案
相关题目
12.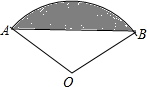 如图所示,扇形AOB的圆心角120°,半径为2,则图中阴影部分的面积为( )
如图所示,扇形AOB的圆心角120°,半径为2,则图中阴影部分的面积为( )
 如图所示,扇形AOB的圆心角120°,半径为2,则图中阴影部分的面积为( )
如图所示,扇形AOB的圆心角120°,半径为2,则图中阴影部分的面积为( )| A. | $\frac{4π}{3}$-2$\sqrt{3}$ | B. | $\frac{4π}{3}$-$\sqrt{3}$ | C. | $\frac{4π}{3}$-$\frac{\sqrt{3}}{2}$ | D. | $\frac{4π}{3}$ |


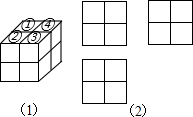 如图,用八个同样大小的小立方体搭成一个大立方体,小明从如图(1)上面的四个小立方体(①②③④)中取走了任意两个后,得到的新几何体的三视图如图(2)所示的概率为$\frac{1}{3}$.
如图,用八个同样大小的小立方体搭成一个大立方体,小明从如图(1)上面的四个小立方体(①②③④)中取走了任意两个后,得到的新几何体的三视图如图(2)所示的概率为$\frac{1}{3}$. 观光塔是潍坊市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是45m,根据以上观测数据可求观光塔的高CD是135m.
观光塔是潍坊市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是45m,根据以上观测数据可求观光塔的高CD是135m.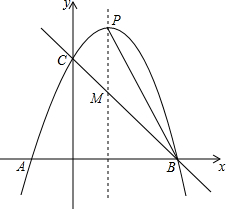 如图,已知抛物线y=-x2+bx+c与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,抛物线的对称轴与抛物线交于点P、与直线BC相交于点M,连接PB.
如图,已知抛物线y=-x2+bx+c与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,抛物线的对称轴与抛物线交于点P、与直线BC相交于点M,连接PB.