题目内容
16. 观光塔是潍坊市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是45m,根据以上观测数据可求观光塔的高CD是135m.
观光塔是潍坊市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是45m,根据以上观测数据可求观光塔的高CD是135m.
分析 根据“爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°”可以求出AD的长,然后根据“在一楼房的底端A点处观测观光塔顶端C处的仰角是60°”可以求出CD的长.
解答 解:∵爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°,
∴∠ADB=30°,
在Rt△ABD中,
tan30°=$\frac{AB}{AD}$,
解得,$\frac{45}{AD}$=$\frac{\sqrt{3}}{3}$,
∴AD=45$\sqrt{3}$,
∵在一楼房的底端A点处观测观光塔顶端C处的仰角是60°,
∴在Rt△ACD中,
CD=AD•tan60°=45$\sqrt{3}$×$\sqrt{3}$=135米.
故答案为135米.
点评 本题考查了解直角三角形的应用--仰角、俯角问题,要求学生能借助仰角、俯角构造直角三角形并解直角三角形.

练习册系列答案
相关题目
7.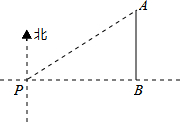 如图,一艘海轮位于灯塔P的北偏东55°方向,距离灯塔2海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向,海轮航行的距离AB长是( )
如图,一艘海轮位于灯塔P的北偏东55°方向,距离灯塔2海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向,海轮航行的距离AB长是( )
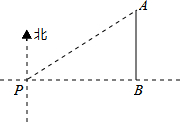 如图,一艘海轮位于灯塔P的北偏东55°方向,距离灯塔2海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向,海轮航行的距离AB长是( )
如图,一艘海轮位于灯塔P的北偏东55°方向,距离灯塔2海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向,海轮航行的距离AB长是( )| A. | 2海里 | B. | 2sin55°海里 | C. | 2cos55°海里 | D. | 2tan55°海里 |
11. 如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若双曲线y=$\frac{k}{x}$与正方形ABCD有公共点,则k的取值范围为( )
如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若双曲线y=$\frac{k}{x}$与正方形ABCD有公共点,则k的取值范围为( )
 如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若双曲线y=$\frac{k}{x}$与正方形ABCD有公共点,则k的取值范围为( )
如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若双曲线y=$\frac{k}{x}$与正方形ABCD有公共点,则k的取值范围为( )| A. | 1<k<9 | B. | 2≤k≤34 | C. | 1≤k≤16 | D. | 4≤k<16 |
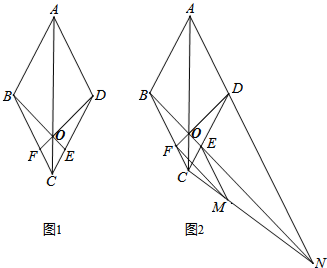
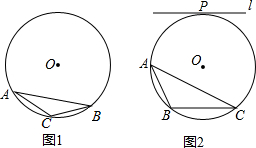 ⊙O为△ABC的外接圆,请仅用无刻度的直尺,根据下列条件分别在图1,图2中画出一条弦,使这条弦将△ABC分成面积相等的两部分(保留作图痕迹,不写作法).
⊙O为△ABC的外接圆,请仅用无刻度的直尺,根据下列条件分别在图1,图2中画出一条弦,使这条弦将△ABC分成面积相等的两部分(保留作图痕迹,不写作法).
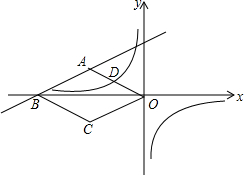 如图,在平面直角坐标系中,四边形ABCO是菱形,B、O在x轴负半轴上,AO=$\sqrt{5}$,tan∠AOB=$\frac{1}{2}$,一次函数y=k1x+b的图象过A、B两点,反比例函数y=$\frac{{k}_{2}}{x}$的图象过OA的中点D.
如图,在平面直角坐标系中,四边形ABCO是菱形,B、O在x轴负半轴上,AO=$\sqrt{5}$,tan∠AOB=$\frac{1}{2}$,一次函数y=k1x+b的图象过A、B两点,反比例函数y=$\frac{{k}_{2}}{x}$的图象过OA的中点D.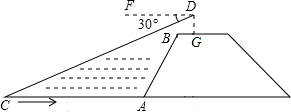 如图,小华站在河岸上的G点,看见河里有一小船沿垂直于岸边的方向划过来.此时,测得小船C的俯角是∠FDC=30°,若小华的眼睛与地面的距离是1.6米,BG=0.7米,BG平行于AC所在的直线,迎水坡i=4:3,坡长AB=8米,点A、B、C、D、F、G在同一平面内,则此时小船C到岸边的距离CA的长为8$\sqrt{3}$-5.5米.(结果保留根号)
如图,小华站在河岸上的G点,看见河里有一小船沿垂直于岸边的方向划过来.此时,测得小船C的俯角是∠FDC=30°,若小华的眼睛与地面的距离是1.6米,BG=0.7米,BG平行于AC所在的直线,迎水坡i=4:3,坡长AB=8米,点A、B、C、D、F、G在同一平面内,则此时小船C到岸边的距离CA的长为8$\sqrt{3}$-5.5米.(结果保留根号)