题目内容
12.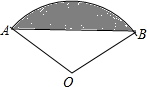 如图所示,扇形AOB的圆心角120°,半径为2,则图中阴影部分的面积为( )
如图所示,扇形AOB的圆心角120°,半径为2,则图中阴影部分的面积为( )| A. | $\frac{4π}{3}$-2$\sqrt{3}$ | B. | $\frac{4π}{3}$-$\sqrt{3}$ | C. | $\frac{4π}{3}$-$\frac{\sqrt{3}}{2}$ | D. | $\frac{4π}{3}$ |
分析 过点O作OD⊥AB,先根据等腰三角形的性质得出∠OAD的度数,由直角三角形的性质得出OD的长,再根据S阴影=S扇形OAB-S△AOB进行计算即可.
解答  解:过点O作OD⊥AB,
解:过点O作OD⊥AB,
∵∠AOB=120°,OA=2,
∴∠OAD=$\frac{180°-∠AOB}{2}$=$\frac{180°-120°}{2}$=30°,
∴OD=$\frac{1}{2}$OA=$\frac{1}{2}$×2=1,AD=$\sqrt{O{A}^{2}-O{D}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∴AB=2AD=2$\sqrt{3}$,
∴S阴影=S扇形OAB-S△AOB=$\frac{360π×{2}^{2}}{360}$-$\frac{1}{2}$×2$\sqrt{3}$×1=$\frac{4π}{3}$-$\sqrt{3}$.
故选:B.
点评 本题考查的是扇形面积的计算及三角形的面积,根据题意得出S阴影=S扇形OAB-S△AOB是解答此题的关键.

练习册系列答案
相关题目
2.事件A:“若a是实数,则|a|≥a”;事件B:“若实数x满足x>-x,则x正实数”.则下列关于事件A和事件B的说法正确的是( )
| A. | 事件A是必然事件,而事件B是随机事件 | |
| B. | 事件A是随机事件,而事件B是必然事件 | |
| C. | 事件A是必然事件,而事件B是必然事件 | |
| D. | 事件A是随机事件,而事件B是随机事件 |
7.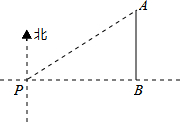 如图,一艘海轮位于灯塔P的北偏东55°方向,距离灯塔2海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向,海轮航行的距离AB长是( )
如图,一艘海轮位于灯塔P的北偏东55°方向,距离灯塔2海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向,海轮航行的距离AB长是( )
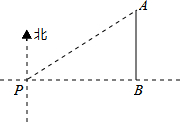 如图,一艘海轮位于灯塔P的北偏东55°方向,距离灯塔2海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向,海轮航行的距离AB长是( )
如图,一艘海轮位于灯塔P的北偏东55°方向,距离灯塔2海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向,海轮航行的距离AB长是( )| A. | 2海里 | B. | 2sin55°海里 | C. | 2cos55°海里 | D. | 2tan55°海里 |
2.据中国新闻网报道,在2014年11月17日公布的全球超级计算机500强榜单中,中国国防科技大学研制的“天河”二号超级计算机,以峰值计算速度每秒5.49亿亿次、持续计算速度每秒3.39亿亿次双精度浮点运算的优异性能位居榜首,第四次摘得全球运行速度最快的超级计算机桂冠.用科学记数法表示“5.49亿亿”,记作( )
| A. | 5.49×1018 | B. | 5.49×1016 | C. | 5.49×1015 | D. | 5.49×1014 |
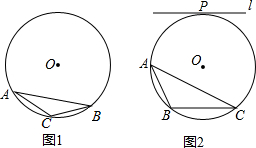 ⊙O为△ABC的外接圆,请仅用无刻度的直尺,根据下列条件分别在图1,图2中画出一条弦,使这条弦将△ABC分成面积相等的两部分(保留作图痕迹,不写作法).
⊙O为△ABC的外接圆,请仅用无刻度的直尺,根据下列条件分别在图1,图2中画出一条弦,使这条弦将△ABC分成面积相等的两部分(保留作图痕迹,不写作法).