题目内容
3. 如图,PA,PB是⊙O的切线,点A、B为切点,AC是⊙O的直径,∠ACB=75°,∠P的度数=30°.
如图,PA,PB是⊙O的切线,点A、B为切点,AC是⊙O的直径,∠ACB=75°,∠P的度数=30°.
分析 连结OB,如图,先利用等腰三角形的性质,由OC=OB得到∠OBC=∠OCB=75°,再利用三角形外角性质求出∠AOB=150°,接着根据切线的性质得到∠OAP=∠OBP=90°,然后根据四边形内角和为360°可计算出∠P的度数.
解答  解:连结OB,如图,
解:连结OB,如图,
∵OC=OB,
∴∠OBC=∠OCB=75°,
∴∠AOB=∠OBC+∠OCB=150°,
∵PA,PB是⊙O的切线,
∴OA⊥PA,OB⊥PB,
∴∠OAP=∠OBP=90°,
∴∠P=180°-∠AOB=30°.
故答案为30°.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
3.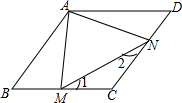 在菱形ABCD中,M,N分别是边BC,CD上的点,且AM=AN=MN=AB,则∠C的度数为( )
在菱形ABCD中,M,N分别是边BC,CD上的点,且AM=AN=MN=AB,则∠C的度数为( )
 在菱形ABCD中,M,N分别是边BC,CD上的点,且AM=AN=MN=AB,则∠C的度数为( )
在菱形ABCD中,M,N分别是边BC,CD上的点,且AM=AN=MN=AB,则∠C的度数为( )| A. | 120° | B. | 100° | C. | 80° | D. | 60° |
8.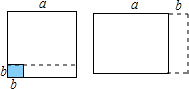 如图,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形.通过计算这两个图形的面积验证了一个等式,这个等式是( )
如图,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形.通过计算这两个图形的面积验证了一个等式,这个等式是( )
 如图,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形.通过计算这两个图形的面积验证了一个等式,这个等式是( )
如图,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形.通过计算这两个图形的面积验证了一个等式,这个等式是( )| A. | (a+2b)(a-b)=a2+ab-2b2 | B. | (a+b)2=a2+2ab+b2 | ||
| C. | a2-b2=(a+b)(a-b) | D. | (a-b)2=a2-2ab-b2. |
13.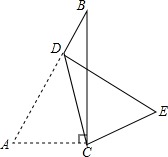 如图,Rt△ABC中,∠ACB=90°,D是边AB上一点,将△ABC沿CD折叠,使点A落在点E的位置,若∠ECB=60°,则∠DCB的度数是( )
如图,Rt△ABC中,∠ACB=90°,D是边AB上一点,将△ABC沿CD折叠,使点A落在点E的位置,若∠ECB=60°,则∠DCB的度数是( )
 如图,Rt△ABC中,∠ACB=90°,D是边AB上一点,将△ABC沿CD折叠,使点A落在点E的位置,若∠ECB=60°,则∠DCB的度数是( )
如图,Rt△ABC中,∠ACB=90°,D是边AB上一点,将△ABC沿CD折叠,使点A落在点E的位置,若∠ECB=60°,则∠DCB的度数是( )| A. | 10° | B. | 12° | C. | 15° | D. | 20° |
 直线y=(a-2)x+b-3在直角坐标系中的图象如图所示,化简|b-a|-$\sqrt{{b}^{2}-6b+9}$-|2-a|=1.
直线y=(a-2)x+b-3在直角坐标系中的图象如图所示,化简|b-a|-$\sqrt{{b}^{2}-6b+9}$-|2-a|=1.
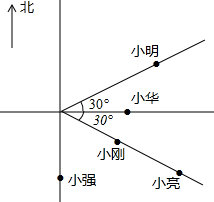 小李、小明、小刚、小强、小华、小亮是很要好的伙伴,他们家的位置如图所示.一天,小李说:“如果以我家为中心,你们各自家的位置在哪儿知道吗?”其余小伙伴说到:“当然知道了.”小李说:“这样吧,你们若回答出下列问题,就证明你们知道.”
小李、小明、小刚、小强、小华、小亮是很要好的伙伴,他们家的位置如图所示.一天,小李说:“如果以我家为中心,你们各自家的位置在哪儿知道吗?”其余小伙伴说到:“当然知道了.”小李说:“这样吧,你们若回答出下列问题,就证明你们知道.”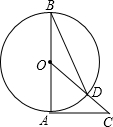 如图,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD,∠C=40°.则∠ABD的度数是25°.
如图,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD,∠C=40°.则∠ABD的度数是25°.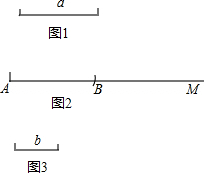 阅读材料:用尺规作图要求作线段AB等于线段a时,小明的具体作法如下:
阅读材料:用尺规作图要求作线段AB等于线段a时,小明的具体作法如下: