题目内容
15.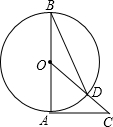 如图,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD,∠C=40°.则∠ABD的度数是25°.
如图,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD,∠C=40°.则∠ABD的度数是25°.
分析 根据切线的性质求出∠OAC,结合∠C=40°求出∠AOC,根据等腰三角形性质求出∠B=∠BDO,根据三角形外角性质求出即可.
解答 解:∵AC是⊙O的切线,
∴∠OAC=90°,
∵∠C=40°,
∴∠AOC=50°,
∵OB=OD,
∴∠ABD=∠BDO,
∵∠ABD+∠BDO=∠AOC,
∴∠ABD=25°,
故答案为:25°.
点评 本题考查了切线的性质,三角形外角性质,三角形内角和定理,等腰三角形性质的应用,解此题的关键是求出∠AOC的度数,题目比较好,难度适中.

练习册系列答案
相关题目
14.2014年12月12日南水北调中线一期工程正式通水.南水北调工程作为缓解北方地区水资源严重短缺局面的重大战略性基础设施,受益人口4.38亿人,总调水规模448亿立方米.其中448亿用科学记数法可表示为( )
| A. | 448×108 | B. | 44.8×109 | C. | 4.48×1010 | D. | 4×1010 |
4.若x+y=3且xy=1,则代数式(2-x)(2-y)的值等于( )
| A. | 2 | B. | 1 | C. | 0 | D. | -1 |
 如图,PA,PB是⊙O的切线,点A、B为切点,AC是⊙O的直径,∠ACB=75°,∠P的度数=30°.
如图,PA,PB是⊙O的切线,点A、B为切点,AC是⊙O的直径,∠ACB=75°,∠P的度数=30°.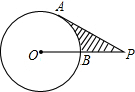 已知:如图,⊙O的半径为2,PA切⊙O于A,OP交⊙O于B,且PA=2$\sqrt{3}$,则阴影部分的面积S=2$\sqrt{3}$-$\frac{2}{3}$π.
已知:如图,⊙O的半径为2,PA切⊙O于A,OP交⊙O于B,且PA=2$\sqrt{3}$,则阴影部分的面积S=2$\sqrt{3}$-$\frac{2}{3}$π.
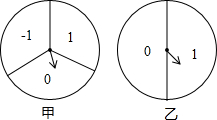 如图,分别转动甲、乙两个转盘各一次(指针落在每一数字区域的机会均等,若指针恰好落在分界线上则重转),当转盘停止时,把甲转盘指针指向的数字作为点A(x,y)的横坐标,把乙转盘指针指向的数字作为点A的纵坐标.
如图,分别转动甲、乙两个转盘各一次(指针落在每一数字区域的机会均等,若指针恰好落在分界线上则重转),当转盘停止时,把甲转盘指针指向的数字作为点A(x,y)的横坐标,把乙转盘指针指向的数字作为点A的纵坐标.