题目内容
8.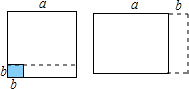 如图,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形.通过计算这两个图形的面积验证了一个等式,这个等式是( )
如图,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形.通过计算这两个图形的面积验证了一个等式,这个等式是( )| A. | (a+2b)(a-b)=a2+ab-2b2 | B. | (a+b)2=a2+2ab+b2 | ||
| C. | a2-b2=(a+b)(a-b) | D. | (a-b)2=a2-2ab-b2. |
分析 利用正方形的面积公式可知剩下的面积=a2-b2,而新形成的矩形是长为a+b,宽为a-b,根据两者相等,即可验证平方差公式.
解答 解:由题意得:a2-b2=(a+b)(a-b).
故选C.
点评 此题主要考查平方差公式,即两个数的和与这两个数的差的积等于这两个数的平方差,这个公式就叫做平方差公式.解决本题的比较两个图形分别表示出面积.

练习册系列答案
相关题目
7.下列所示的四个图形中,∠1和∠2不是同位角的是( )
| A. |  | B. |  | C. |  | D. |  |
5.直线y=kx-4经过点(-2,2),则该直线的解析式是( )
| A. | y=x-4 | B. | y=-x-4 | C. | y=-3x-4 | D. | y=3x-4 |
18.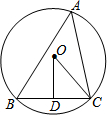 如图,△ABC内接于⊙O,OD⊥BC于D,∠A=50°,则∠COD的度数是( )
如图,△ABC内接于⊙O,OD⊥BC于D,∠A=50°,则∠COD的度数是( )
 如图,△ABC内接于⊙O,OD⊥BC于D,∠A=50°,则∠COD的度数是( )
如图,△ABC内接于⊙O,OD⊥BC于D,∠A=50°,则∠COD的度数是( )| A. | 60° | B. | 50° | C. | 45° | D. | 40° |
 如图,PA,PB是⊙O的切线,点A、B为切点,AC是⊙O的直径,∠ACB=75°,∠P的度数=30°.
如图,PA,PB是⊙O的切线,点A、B为切点,AC是⊙O的直径,∠ACB=75°,∠P的度数=30°. 如图是由若干个边长为a的大小相同的小正方体组成的几何体,这个几何体的表面积是28a2.(用a的代数式表示)
如图是由若干个边长为a的大小相同的小正方体组成的几何体,这个几何体的表面积是28a2.(用a的代数式表示) 如图,将△ABC沿DE折叠,使点A与BC边的中点F重合,有下面四个结论:
如图,将△ABC沿DE折叠,使点A与BC边的中点F重合,有下面四个结论: