题目内容
已知,关于x的方程(k2-1)x2+2kx+4=0的一个根是-2,试确定k的值,并求出它的另一个根.
考点:一元二次方程的解,根与系数的关系
专题:
分析:把x=-2代入方程,得到一个关于k的方程,解方程求得k的值,再将k的值代入原方程求解即可.
解答:解:把x=-2代入方程(k2-1)x2+2kx+4=0,
可得4(k2-1)-4k+4=0,
整理,得k2-k=0,
解得k=1或k=0.
∵k2-1≠0,
∴k=1不符合题意,
∴k=0.
把k=0代入原方程可得-x2+4=0,
解得x1=2,x2=-2.
∴k的值为0,它的另一个根为2.
可得4(k2-1)-4k+4=0,
整理,得k2-k=0,
解得k=1或k=0.
∵k2-1≠0,
∴k=1不符合题意,
∴k=0.
把k=0代入原方程可得-x2+4=0,
解得x1=2,x2=-2.
∴k的值为0,它的另一个根为2.
点评:本题考查了一元二次方程、一元二次方程的解的定义以及一元二次方程的解法,是基础知识,需熟练掌握.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 如图,⊙O是△ABC的外接圆,∠OCB=50°,则∠A的度数等于( )
如图,⊙O是△ABC的外接圆,∠OCB=50°,则∠A的度数等于( )| A、40° | B、50° |
| C、60° | D、70° |
使函数y=
有意义的自变量x的取值范围为( )
| ||
| x |
| A、x≠0 |
| B、x≥-1 |
| C、x≥-1且x≠0 |
| D、x>-1且x≠0 |
一个面积为120的矩形苗圃,它的长比宽多2米,则苗圃长是( )
| A、10 | B、12 | C、13 | D、14 |
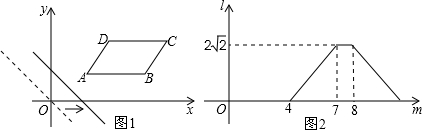
 如图,在四边形ABCD中,已知AD∥BC,∠C=90°,CD=8cm,BC=24cm,AD=26cm,点P从点C出发,以1cm/s的速度向点B运动;点Q从点A同时出发,以3cm/s的速度向点D运动.规定其中一个动点到达端点时,另一个动点也随之停止运动,从运动开始,需经过多少时间能使四边形ABPQ为平行四边形?并说明理由.
如图,在四边形ABCD中,已知AD∥BC,∠C=90°,CD=8cm,BC=24cm,AD=26cm,点P从点C出发,以1cm/s的速度向点B运动;点Q从点A同时出发,以3cm/s的速度向点D运动.规定其中一个动点到达端点时,另一个动点也随之停止运动,从运动开始,需经过多少时间能使四边形ABPQ为平行四边形?并说明理由. 如图,已知AD平分∠BAC,且AD⊥BC于D,点E,A,C在同一直线上,∠DAC=∠EFA,延长EF交BC于G,
如图,已知AD平分∠BAC,且AD⊥BC于D,点E,A,C在同一直线上,∠DAC=∠EFA,延长EF交BC于G, 已知:长方形ABCD中有两个小正方形甲和乙,甲的面积为2,乙的面积为9
已知:长方形ABCD中有两个小正方形甲和乙,甲的面积为2,乙的面积为9