题目内容
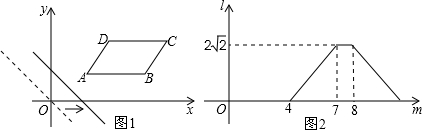
如图1,在平面直角坐标系中,将?ABCD放置在第一象限,且AB∥x轴.直线y=-x从原点出发沿x轴正方向平移,在平移过程中直线被平行四边形截得的线段长度l与直线在x轴上平移的距离m的函数图象如图2,那么ABCD面积为( )

| A、4 | ||
B、4
| ||
| C、8 | ||
D、8
|
考点:动点问题的函数图象
专题:动点型,数形结合
分析:根据图象可以得到当移动的距离是4时,直线经过点A,当移动距离是7时,直线经过D,在移动距离是8时经过B,则AB=8-4=4,当直线经过D点,设交AB与N,则DN=2
,作DM⊥AB于点M.利用三角函数即可求得DM即平行四边形的高,然后利用平行四边形的面积公式即可求解.
| 2 |
解答:解:根据图象可以得到当移动的距离是4时,直线经过点A,当移动距离是7时,直线经过D,在移动距离是8时经过B,
则AB=8-4=4,
当直线经过D点,设交AB与N,则DN=2
,作DM⊥AB于点M.
∵y=-x与x轴形成的角是45°,
又∵AB∥x轴,
∴∠DNM=45°,
∴DM=DN•sin45°=2
×
=2,
则平行四边形的面积是:AB•DM=4×2=8.
故选:C.
则AB=8-4=4,
当直线经过D点,设交AB与N,则DN=2
| 2 |
∵y=-x与x轴形成的角是45°,
又∵AB∥x轴,
∴∠DNM=45°,
∴DM=DN•sin45°=2
| 2 |
| ||
| 2 |
则平行四边形的面积是:AB•DM=4×2=8.
故选:C.
点评:本题考查了函数的图象,根据图象理解AB的长度,正确求得平行四边形的高是关键.

练习册系列答案
 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
下列调查中,适合采用全面调查(普查)方式的是( )
| A、对长江河水质情况的调查 |
| B、对重庆新开张的宜家家居每天客流量的调查 |
| C、对乘坐某航班旅客的安全检查 |
| D、对某类烟花爆竹燃放安全情况的调查 |
下列调查中,事宜采用全面调查(普查)方式的是( )
| A、环境保护部门了解兰州自来水污染情况 |
| B、了解某种水果的甜度和水量 |
| C、了解外地游客对我市旅游景点“磁器口”的满意程度 |
| D、了解我班同学的中考体育成绩 |
 如图,将周长为8的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为( )
如图,将周长为8的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为( )| A、6 | B、8 | C、10 | D、12 |
 已知:某学校的平面示意图如图,如果旗杆所在位置为(-3,2),请你画出正确的平面直角坐标系,并写出校门、新教学楼、英语办的位置坐标来.
已知:某学校的平面示意图如图,如果旗杆所在位置为(-3,2),请你画出正确的平面直角坐标系,并写出校门、新教学楼、英语办的位置坐标来.