题目内容
 某露天游泳池对外开放时,收入以出售门票的方式获得,每天各项开支的总成本是固定的,一天内盈利y(元)与购票进场的人数x(人)之间的函数关系如图所示.为保证游泳时的安全与卫生,管理部门对每天进入游泳池的人数进行了限制.
某露天游泳池对外开放时,收入以出售门票的方式获得,每天各项开支的总成本是固定的,一天内盈利y(元)与购票进场的人数x(人)之间的函数关系如图所示.为保证游泳时的安全与卫生,管理部门对每天进入游泳池的人数进行了限制.根据图象回答下列问题:
(1)管理部门规定一天内游泳池的最大容量是多少?经营者一天内的最高盈利是多少?
(2)一天内出售多少门票时,经营者才能保证不亏损?要使一天内的盈利在600元以上,至少要出售多少张门票?
(3)盈利为什么能取负值?-200的含义是什么?
考点:一次函数的应用
专题:
分析:(1)由函数图象的数据可以得出管理部门规定一天内游泳池的最大容量是250人,经营者一天内的最高盈利是800元;
(2)由函数图象的数据可以得出一天内出售50门票时,经营者才能保证不亏损,要使一天内的盈利在600元以上,至少要出售200张门票;
(3)由题意可以得出盈利为负值,是表示亏损;-200的含义是表示亏损200元.
(2)由函数图象的数据可以得出一天内出售50门票时,经营者才能保证不亏损,要使一天内的盈利在600元以上,至少要出售200张门票;
(3)由题意可以得出盈利为负值,是表示亏损;-200的含义是表示亏损200元.
解答:解:(1)由题意,得
管理部门规定一天内游泳池的最大容量是250人,经营者一天内的最高盈利是800元;
(2)由题意,得
一天内出售50门票时,经营者才能保证不亏损.要使一天内的盈利在600元以上,至少要出售200张门票;
(3)由题意,得
盈利为负值,是表示亏损;-200的含义是表示亏损200元.
管理部门规定一天内游泳池的最大容量是250人,经营者一天内的最高盈利是800元;
(2)由题意,得
一天内出售50门票时,经营者才能保证不亏损.要使一天内的盈利在600元以上,至少要出售200张门票;
(3)由题意,得
盈利为负值,是表示亏损;-200的含义是表示亏损200元.
点评:本题考查了一次函数的图象的运用,一次函数的性质的运用,解答时理解函数图象的数据的含义是解答本题的关键.

练习册系列答案
相关题目
在矩形ABCD中,AB=4,AD=2,O是CD的中点,以点O为圆心画图,使得A,B,C,D四点中有两点在圆内,有两点在圆外,则⊙O的半径r的取值范围是( )
A、2
| ||
B、2<r<2
| ||
| C、2<r<3 | ||
| D、3<r<4 |
 如图,点M在射线OA上,点N在射线OB上,芳芳在直线MN上求作一点P,使它到OA、OB的距离相等,则点P是( )
如图,点M在射线OA上,点N在射线OB上,芳芳在直线MN上求作一点P,使它到OA、OB的距离相等,则点P是( )| A、线段MN的中点 |
| B、OA与OB的中垂线的交点 |
| C、OA与MN的中垂线的交点 |
| D、MN与∠AOB的平分线的交点 |
 探索规律:观察如图由“※”组成的图案和算式,解答问题:
探索规律:观察如图由“※”组成的图案和算式,解答问题: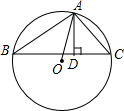 如图,已知△ABC内接于⊙O,AD为BC边上的高.
如图,已知△ABC内接于⊙O,AD为BC边上的高.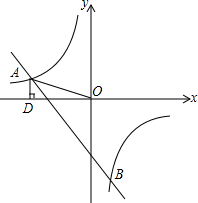 如图,一次函数y=kx+b的图象与反比例函数y=
如图,一次函数y=kx+b的图象与反比例函数y= 如图,在每个小正方形的边长均为1个单位长度的方格纸中,有一个△ABC,△ABC的三个顶点均与小正方形的顶点重合.
如图,在每个小正方形的边长均为1个单位长度的方格纸中,有一个△ABC,△ABC的三个顶点均与小正方形的顶点重合.