题目内容
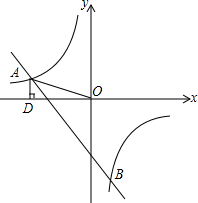 如图,一次函数y=kx+b的图象与反比例函数y=
如图,一次函数y=kx+b的图象与反比例函数y=| m |
| x |
| 5 |
(1)求反比例函数的解析式;
(2)求一次函数的解析式.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)设AD=x>0,由OD=2AD=2x得A(-2x,x).根据OA=
列出方程x2+(2x)2=5,解方程求出x的值,得到A点坐标,再将A点坐标代入y=
,利用待定系数法即可求出反比例函数的解析式;
(2)先把xB=0.5代入y=-
,求出yB=-
=-4,那么B点坐标为(0.5,-4).再将A、B两点的坐标代入y=kx+b,利用待定系数法即可求出一次函数的解析式.
| 5 |
| m |
| x |
(2)先把xB=0.5代入y=-
| 2 |
| x |
| 2 |
| 0.5 |
解答:解:(1)设AD=x>0,则OD=2AD=2x,A(-2x,x).
∵OA=
,
∴x2+(2x)2=5,
∴x=±1(负值舍去),
∴A(-2,1).
∵反比例函数y=
的图象经过A点,
∴1=
,
∴m=-2,
∴反比例函数的解析式为y=-
;
(2)∵y=-
,
∴当xB=0.5时,yB=-
=-4,
∴B点坐标为(0.5,-4).
∵一次函数y=kx+b的图象经过A、B两点,
∴
,
解得
,
∴一次函数解析式为y=-2x-3.
∵OA=
| 5 |
∴x2+(2x)2=5,
∴x=±1(负值舍去),
∴A(-2,1).
∵反比例函数y=
| m |
| x |
∴1=
| m |
| -2 |
∴m=-2,
∴反比例函数的解析式为y=-
| 2 |
| x |
(2)∵y=-
| 2 |
| x |
∴当xB=0.5时,yB=-
| 2 |
| 0.5 |
∴B点坐标为(0.5,-4).
∵一次函数y=kx+b的图象经过A、B两点,
∴
|
解得
|
∴一次函数解析式为y=-2x-3.
点评:本题考查了反比例函数与一次函数的交点问题,函数图象上点的坐标特征,掌握待定系数法是解题的关键.

练习册系列答案
相关题目
下列结论错误的个数是( )
①若a>0,b>0,则a+b>0;
②若a<0,b<0,则a+b<0;
③若a>0,b>0,则a+b>0.
①若a>0,b>0,则a+b>0;
②若a<0,b<0,则a+b<0;
③若a>0,b>0,则a+b>0.
| A、0个 | B、1个 | C、2个 | D、3个 |
平面内有五个点,过每两个点作一条直线,可以作几条直线?( )
| A、1条、4条、8条或10条 |
| B、1条、5条、9条或10条 |
| C、1条、5条、8条或10条 |
| D、1条或10条 |
如图所示是四位同学所画的数轴,其中正确的是( )
A、 |
B、 |
C、 |
D、 |
下列各组中的四条线段,其中成比例的是( )
| A、5cm,3cm,4cm,1cm | ||||||||
| B、3cm,5cm,9cm,13cm | ||||||||
| C、a:b:c:d=1:2:3:4 | ||||||||
D、
|
 如图,已知y=x2-x-3的图象,请求出方程x2-x-3=0的近似解.
如图,已知y=x2-x-3的图象,请求出方程x2-x-3=0的近似解. 某露天游泳池对外开放时,收入以出售门票的方式获得,每天各项开支的总成本是固定的,一天内盈利y(元)与购票进场的人数x(人)之间的函数关系如图所示.为保证游泳时的安全与卫生,管理部门对每天进入游泳池的人数进行了限制.
某露天游泳池对外开放时,收入以出售门票的方式获得,每天各项开支的总成本是固定的,一天内盈利y(元)与购票进场的人数x(人)之间的函数关系如图所示.为保证游泳时的安全与卫生,管理部门对每天进入游泳池的人数进行了限制.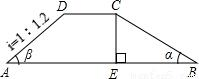 如图,水坝的横截面积是梯形ABCD,迎水坡BC的坡角α为30°,背水坡AD的坡度i,即(tanβ)为1:1.2,坝顶宽DC=2.5m,坝高4.5m.
如图,水坝的横截面积是梯形ABCD,迎水坡BC的坡角α为30°,背水坡AD的坡度i,即(tanβ)为1:1.2,坝顶宽DC=2.5m,坝高4.5m.