题目内容
 如图(1),BP、CP分别是△ABC的内、外角平分线.
如图(1),BP、CP分别是△ABC的内、外角平分线.(1)若∠A=60°,则∠P=
(2)如图(2),过B作直线MQ,交PC的延长线于Q,且使∠MBA=∠QBC.试讨论当∠A满足什么条件时,∠P>∠Q;∠P=∠Q;∠P<∠Q.
考点:三角形内角和定理,三角形的外角性质
专题:
分析:(1)根据角平分线的定义得∠PBC=
∠ABC,∠PCD=
∠ACD,再根据三角形外角性质得∠ACD=∠A+∠ABC,∠PCD=∠PBC+∠P,所以
(∠A+∠ABC)=∠PBC+∠P=
∠ABC+∠P,然后整理可得∠P=
∠A=30°.
(2)由于∠P=
∠A,∠P+∠Q=90°,代入∠P>∠Q;∠P=∠Q;∠P<∠Q.即可求得.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)由于∠P=
| 1 |
| 2 |
解答:解:(1)∵△ABC的内角平分线BP与外角平分线CP交于P,
∴∠PBC=
∠ABC,∠PCD=
∠ACD,
∵∠ACD=∠A+∠ABC,∠PCD=∠PBC+∠P,
∴
(∠A+∠ABC)=∠PBC+∠P=
∠ABC+∠P,
∴∠P=
∠A=
×60°=30°.
(2)∵∠P=
∠A,
∴要使∠P>∠Q,则
∠A>∠Q,
∵∠ABP=∠CBP,∠MBA=∠QBC,
∴∠P+∠Q=90°,
∴
∠A+∠Q=90°,
∴∠Q=90°-
∠A,
∴
∠A>90°-
∠A,即∠A>90°,
∴要使∠P>∠Q,∠A=90°,要使∠P>∠Q,∠A<90°.
∴∠PBC=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠ACD=∠A+∠ABC,∠PCD=∠PBC+∠P,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴∠P=
| 1 |
| 2 |
| 1 |
| 2 |
(2)∵∠P=
| 1 |
| 2 |
∴要使∠P>∠Q,则
| 1 |
| 2 |
∵∠ABP=∠CBP,∠MBA=∠QBC,
∴∠P+∠Q=90°,
∴
| 1 |
| 2 |
∴∠Q=90°-
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴要使∠P>∠Q,∠A=90°,要使∠P>∠Q,∠A<90°.
点评:本题考查了三角形内角和定理:三角形内角和是180°.也考查了三角形外角性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
等腰三角形底边和底边上的高之和等于其外接圆直径,则它的底边和底边上的高之比为( )
| A、1:2 | B、2:1 |
| C、1:4 | D、4:1 |
 小军在想这个问题:如图,已知ADB是一条直线,∠ADE=∠ABC,且DG、BF分别是∠ADE和∠ABC的平分线,试猜想DG、BF的位置关系.小明看了一下,便说DG、BF一定平行;小军想了一会还是没有想通,你能帮助说明理由吗?
小军在想这个问题:如图,已知ADB是一条直线,∠ADE=∠ABC,且DG、BF分别是∠ADE和∠ABC的平分线,试猜想DG、BF的位置关系.小明看了一下,便说DG、BF一定平行;小军想了一会还是没有想通,你能帮助说明理由吗?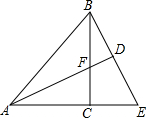 如图,BC为△ABE的高,F在BC上,且AC=BC,CE=CF,延长AF交BE于D,若AB=AE,且BE=8cm.求△AFB的面积.
如图,BC为△ABE的高,F在BC上,且AC=BC,CE=CF,延长AF交BE于D,若AB=AE,且BE=8cm.求△AFB的面积.