题目内容
如图，△ABC中，BE平分∠ABC，DE∥BC交于AB于点D，BC=6，AB=9，求DE的长．考点：相似三角形的判定与性质
专题：
分析：由BE平分∠ABC，可求得DE=BD，设DE为x，则BD=x，AD=AB-BD=9-x，再由平行线分线段成比例性质可得
=
，代入可求得DE的长．
| AD |
| AB |
| DE |
| BC |
解答：解：∵BE平分∠ABC，
∴∠DBE=∠CBE，
∵DE∥BC，
∴∠DEB=∠CBE，
∴∠DEB=∠DBE，
∴DE=BD，
设DE=x，则BD=x，AD=AB-BD=9-x，
又∵DE∥BC，
∴
=
，
∴
=
，
解得x=3.6．
∴∠DBE=∠CBE，
∵DE∥BC，
∴∠DEB=∠CBE，
∴∠DEB=∠DBE，
∴DE=BD，
设DE=x，则BD=x，AD=AB-BD=9-x，
又∵DE∥BC，
∴
| AD |
| AB |
| DE |
| BC |
∴
| 9-x |
| 9 |
| x |
| 6 |
解得x=3.6．
点评：本题主要考查平行线分线段成比例性质的运用，解题的关键是证得DE=BD．
练习册系列答案
相关题目
小军在想这个问题：如图，已知ADB是一条直线，∠ADE=∠ABC，且DG、BF分别是∠ADE和∠ABC的平分线，试猜想DG、BF的位置关系．小明看了一下，便说DG、BF一定平行；小军想了一会还是没有想通，你能帮助说明理由吗？
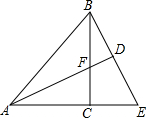如图，BC为△ABE的高，F在BC上，且AC=BC，CE=CF，延长AF交BE于D，若AB=AE，且BE=8cm．求△AFB的面积．
如图，已知弦AB、CD相交于P点，且∠AOC=44°，∠BOD=46°．则∠APC的度数是