题目内容
 如图,已知:C是以AB为直径的半圆O上一点,CF⊥AB于点F,直线AC与过B点的切线相交于点D,E为BD中点,连接AE交CF于点H,连接CE.
如图,已知:C是以AB为直径的半圆O上一点,CF⊥AB于点F,直线AC与过B点的切线相交于点D,E为BD中点,连接AE交CF于点H,连接CE.(1)求证:点H是CF中点;
(2)求证:CE是⊙O的切线;
(3)若⊙O的半径为2,BE=3,求CF的长.
考点:切线的判定,相似三角形的判定与性质
专题:证明题
分析:(1)根据切线的性质得AB⊥BD,而CF⊥AB,所以CF∥BD,根据相似的判定方法得△AFH∽△ABE,△AHC∽△AED,利用相似的性质得
=
,
=
,所以
=
,而BE=DE,则FH=CH;
(2)根据圆周角定理由AB为⊙的直径得∠ACB=90°,则∠BCD=90°,而CE为BD边上的中线,根据直角三角形斜边上的中线性质得CE=BE=DE,则∠2=∠3,而∠1=∠4,所以有∠1+∠2=∠3+∠4,即∠OCE=∠OBE=90°,则OC⊥CE,然后根据切线的判定定理得CE是⊙O的切线;
(3)先计算出BD=2BE=6,在Rt△ABD中,根据勾股定理计算出AD=2
,再证明Rt△ABC∽Rt△ADB,利用相似比计算出AC=
,然后证明△ACF∽△ADB,利用相似比可计算出CF=
.
| FH |
| BE |
| AH |
| AE |
| CH |
| DE |
| AH |
| AE |
| FH |
| BE |
| CH |
| DE |
(2)根据圆周角定理由AB为⊙的直径得∠ACB=90°,则∠BCD=90°,而CE为BD边上的中线,根据直角三角形斜边上的中线性质得CE=BE=DE,则∠2=∠3,而∠1=∠4,所以有∠1+∠2=∠3+∠4,即∠OCE=∠OBE=90°,则OC⊥CE,然后根据切线的判定定理得CE是⊙O的切线;
(3)先计算出BD=2BE=6,在Rt△ABD中,根据勾股定理计算出AD=2
| 13 |
8
| ||
| 13 |
| 24 |
| 13 |
解答:(1)证明:∵BD为⊙的切线,
∴AB⊥BD,
∵CF⊥AB,
∴CF∥BD,
∴△AFH∽△ABE,△AHC∽△AED,
∴
=
,
=
,
∴
=
,
而E为BD中点,
∴BE=DE,
∴FH=CH,
即点H是CF中点;
(2)证明:∵AB为⊙的直径,
 ∴∠ACB=90°,
∴∠ACB=90°,
∴∠BCD=90°,
而CE为BD边上的中线,
∴CE=BE=DE,
∴∠2=∠3,
∵OB=OC,
∴∠1=∠4,
∴∠1+∠2=∠3+∠4,即∠OCE=∠OBE=90°,
∴OC⊥CE,
∴CE是⊙O的切线;
(3)解:∵BE=3,
∴BD=2BE=6,
在Rt△ABD中,AB=4,
∴AD=
=2
,
∵∠BAC=∠DAB,
∴Rt△ABC∽Rt△ADB,
∴
=
,即
=
,
∴AC=
,
∵CF∥BD,
∴△ACF∽△ADB,
∴
=
,即
=
,
∴CF=
.
∴AB⊥BD,
∵CF⊥AB,
∴CF∥BD,
∴△AFH∽△ABE,△AHC∽△AED,
∴
| FH |
| BE |
| AH |
| AE |
| CH |
| DE |
| AH |
| AE |
∴
| FH |
| BE |
| CH |
| DE |
而E为BD中点,
∴BE=DE,
∴FH=CH,
即点H是CF中点;
(2)证明:∵AB为⊙的直径,
 ∴∠ACB=90°,
∴∠ACB=90°,∴∠BCD=90°,
而CE为BD边上的中线,
∴CE=BE=DE,
∴∠2=∠3,
∵OB=OC,
∴∠1=∠4,
∴∠1+∠2=∠3+∠4,即∠OCE=∠OBE=90°,
∴OC⊥CE,
∴CE是⊙O的切线;
(3)解:∵BE=3,
∴BD=2BE=6,
在Rt△ABD中,AB=4,
∴AD=
| AB2+BD2 |
| 13 |
∵∠BAC=∠DAB,
∴Rt△ABC∽Rt△ADB,
∴
| AC |
| AB |
| AB |
| AD |
| AC |
| 4 |
| 4 | ||
2
|
∴AC=
8
| ||
| 13 |
∵CF∥BD,
∴△ACF∽△ADB,
∴
| CF |
| BD |
| AC |
| AD |
| CF |
| 6 |
| ||||
2
|
∴CF=
| 24 |
| 13 |
点评:本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了相似三角形的判定与性质、圆周角定理和勾股定理.

练习册系列答案
相关题目
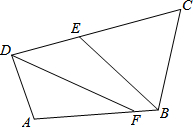 如图,在四边形ABCD中,∠ABC、∠ADC的平分线分别与CD、AB相交于点E、F.
如图,在四边形ABCD中,∠ABC、∠ADC的平分线分别与CD、AB相交于点E、F. 如图,点E、F、G、H分别在菱形ABCD的四条边上,且BE=BF=DG=DH,连接EF,FG,GH,HE得到四边形EFGH.
如图,点E、F、G、H分别在菱形ABCD的四条边上,且BE=BF=DG=DH,连接EF,FG,GH,HE得到四边形EFGH. 如图,已知点A1,A2,…,A2014在函数y=2x2位于第二象限的图象上,点B1,B2,…,B2014在函数y=2x2位于第一象限的图象上,点C1,C2,…,C2014在y轴的正半轴上,若四边形OA1C1B1、C1A2C2B2,…,C2013A2014C2014B2014都是正方形,则正方形C2013A2014C2014B2014的边长为
如图,已知点A1,A2,…,A2014在函数y=2x2位于第二象限的图象上,点B1,B2,…,B2014在函数y=2x2位于第一象限的图象上,点C1,C2,…,C2014在y轴的正半轴上,若四边形OA1C1B1、C1A2C2B2,…,C2013A2014C2014B2014都是正方形,则正方形C2013A2014C2014B2014的边长为 如图所示,∠1与∠2的关系是
如图所示,∠1与∠2的关系是