Question

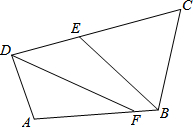如图，在四边形ABCD中，∠ABC、∠ADC的平分线分别与CD、AB相交于点E、F．
（1）若∠A与∠C互补，∠CDF=40°，求∠ABE的度数．
（2）若∠A=∠C=90°，试判断DF与BE有怎样的位置关系，并请说明理由．

Answer 1

考点：平行线的判定,余角和补角

专题：常规题型

分析：（1）根据四边形内角和得到∠ABC+∠ADC=180°，再根据角平分线定义得到∠ABE=

1

2

∠ABC，∠CDF=

1

2

∠ADC，而∠CDF=40°，则∠ADC=80°，所以2∠ABE+80°=180°，解得∠ABE=50°；
（2）根据四边形内角和得到∠ABC+∠ADC=180°，再根据角平分线定义得到∠ABE=

1

2

∠ABC，∠ADF=

1

2

∠ADC，则∠ABE+∠ADF=90°，加上∠AFD+∠ADF=90°，利用等角的余角相等得∠AFD=∠ABE，然后根据平行线的判定定理得到DF∥BE．

解答：解：（1）∵在四边形ABCD中，∠A与∠C互补，
∴∠ABC+∠ADC=180°，
∵∠ABC、∠ADC的平分线分别与CD、AB相交于点E、F．
∴∠ABE=

1

2

∠ABC，∠CDF=

1

2

∠ADC，
而∠CDF=40°，
∴∠ADC=2×40°=80°，
∴2∠ABE+80°=180°，
∴∠ABE=50°；
（2）DF与BE平行．
理由如下：
∵在四边形ABCD中，∠A=∠C=90°，
∴∠ABC+∠ADC=180°，
∵∠ABC、∠ADC的平分线分别与CD、AB相交于点E、F．
∴∠ABE=

1

2

∠ABC，∠ADF=

1

2

∠ADC，
∴∠ABE+∠ADF=90°，
而∠AFD+∠ADF=90°，
∴∠AFD=∠ABE，
∴DF∥BE．

点评：本题考查了平行线的判定：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行．也考查了补角和余角．