题目内容
已知k=
=
=
(a+b+c≠0),且
+n2+4=4n,则关于y与x的一次函数y=kx+m+n的图象一定经过第 象限.
| a+b-c |
| c |
| a-b+c |
| b |
| -a+b+c |
| a |
| m+3 |
考点:一次函数图象与系数的关系,非负数的性质:偶次方,非负数的性质:算术平方根,比例的性质
专题:
分析:利用等比性质求得k可能的值,把含m,n的等式整理为两个非负数的和的形式,即可得到m,n准确的值,进而根据一次函数图象的性质得到一定经过的象限.
解答:解:∵
+n2+4=4n,
∴
+n2+4-4n=0,
∴
+(n-2)2=0,
∴m+3=0,n-2=0,
∴m=-3,n=2,
∴m+n=-1,
∵a+b+c≠0时,
k=
=
=1,
此时一次函数经过一、三、四象限;
∴关于y与x的一次函数y=kx+m+n的图象一定经过第一、三、四象限.
故答案为:一、三、四.
| m+3 |
∴
| m+3 |
∴
| m+3 |
∴m+3=0,n-2=0,
∴m=-3,n=2,
∴m+n=-1,
∵a+b+c≠0时,
k=
| a+b-c+a-b+c-a+b+c |
| a+b+c |
| a+b+c |
| a+b+c |
此时一次函数经过一、三、四象限;
∴关于y与x的一次函数y=kx+m+n的图象一定经过第一、三、四象限.
故答案为:一、三、四.
点评:此题主要考查了比例性质的应用及一次函数图象的性质;分类探讨出t可能的值是解决本题的突破点;用到的知识点为:一次函数的比例系数,常数项均大于0,图象经过一、二、三象限;一次函数的比例系数,常数项均小于0,图象经过二、三、四象限;

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案
相关题目
 (1)阅读下面材料:
(1)阅读下面材料: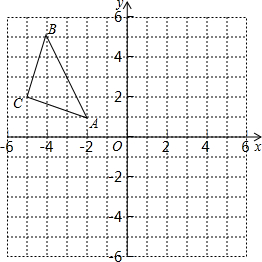 如图,△ABC在平面直角坐标系中,点A、B、C的坐标分别为A(-2,1),B(-4,5),C(-5,2).
如图,△ABC在平面直角坐标系中,点A、B、C的坐标分别为A(-2,1),B(-4,5),C(-5,2). 如图,已知:C是以AB为直径的半圆O上一点,CF⊥AB于点F,直线AC与过B点的切线相交于点D,E为BD中点,连接AE交CF于点H,连接CE.
如图,已知:C是以AB为直径的半圆O上一点,CF⊥AB于点F,直线AC与过B点的切线相交于点D,E为BD中点,连接AE交CF于点H,连接CE.