题目内容
如图，在Rt△ABC中，∠ACB=90°，∠B=30°，AD平分∠CAB．
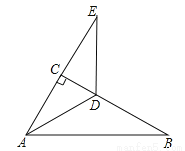
（1）求∠CAD的度数；
（2）延长AC至E，使CE=AC，求证：DA=DE．
30°；见解析．
【解析】试题分析：根据∠ACB和∠B的度数得出∠CAB的度数，根据角平分线的性质得出∠CAD的度数；根据∠ACD+∠ECD=180°，∠ACD=90°得出∠ACD=∠ECD=90°，证明△ACD和△ECD全等，从而得出结论．
试题解析：（1）∵在Rt△ABC中，∠ACB=90°，∠B=30°， ∴∠CAB=60°．
又∵AD平分∠CAB， ∴∠CAD=∠CAB=...
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
在我们常见的英文字母中,也存在着同位角、内错角、同旁内角,在下面几个字母中,含有内错角最少的字母是( )
A. 
B. 
C. 
D. 
C
【解析】根据内错角的定义可知H中含有2对内错角，M中含有2对内错角；N中含有1对，A中含有2对内错角.
故选：C. 已知，如图，四边形ABCD中．AB=AD，CB=CD，AC与BD交于点E．求证：（1）∠1=∠2；（2）AC⊥BD．
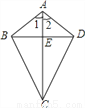
（1）证明见解析（2）证明见解析
【解析】试题分析：（1）由SSS证明△ABC≌△ADC，得出对应角相等即可；
（2）由线段垂直平分线的性质定理的逆定理得出点A在BD的垂直平分线上，点C在BD的垂直平分线上，得出AC垂直平分BD即可．
试题解析：（1）在△ABC和△ADC中，
，
∴△ABC≌△ADC（SSS），
∴∠1=∠2；
（2）∵AB=AD，CB=... 如图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,指出其他的对应边和对应角.
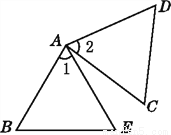
见解析
【解析】试题分析：先根据△ABE≌△ACD，可以确定点A的对应点是A，点B的对应点是C，点D的对应点是E，然后根据对应顶点，结合图形即可找出对应边和对应角.
试题解析：∵△ABE≌△ACD，∠1=∠2，∠B=∠C，
∴点A的对应点是A，点B的对应点是C，点E的对应点是D，
∴∠BAE与∠CAD是对应角，AB与AC，BE与CD，AD与AE是对应边. 如图,沿直线AC对折,△ABC与△ADC重合,则△ABC≌___________,AB的对应边是___________,∠BCA的对应角是___________.
△ADC AD ∠DCA
【解析】本题考查的是全等三角形的性质
根据全等三角形的对应边相等、对应角相等即可判断， 如图，在△ABC中，BD是边AC上的中线，E是BC的中点，连接DE.如果△BDE的面积为2，那么△ABC的面积为______．
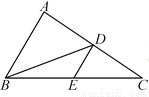
8
【解析】∵E是BC的中点,
∴ ,
∵BD是边AC上的中线,
∴ ,
∴,
又△BDE的面积为2，
∴△ABC的面积为8；
故答案是：8. 如图，∠A＝∠B，∠C＝α，DE⊥AC，FD⊥AB，则∠EDF等于( )
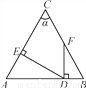
A. α B. 90°－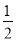
α C. 90°－α D. 180°－2α
B
【解析】∵∠A=∠B，∠C=α，
∴∠A=∠B=（180°-α），
∵DE⊥AC，FD⊥AB，
∴∠AED=∠FDB=90°，
∴∠ADE=90°-（180°-α）=α，
∴∠EDF =180°-90°-α=90°-α，
故选B． 单项式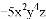
的系数是________，次数是 _______.
-5 7
【解析】单项式中的数字因数是单项式的系数，所有字母的指数的和叫做这个单项式的次数.由此可得单项式的系数是-5，次数是7. 我们规定，若关于x的一元一次方程ax=b的解为b﹣a，则称该方程为“差解方程”，例如：2x=4的解为2，且2=4﹣2，则该方程2x﹣4是差解方程．
（1）判断3x=4.5是否是差解方程；
（2）若关于x的一元一次方程5x=m+1是差解方程，求m的值．
（1）是；（2）m的值为．
【解析】试题分析：（1）求出方程的解，根据差解方程的意义得出即可；
（2）根据差解方程得出关于的方程，求出方程的解即可．
试题解析：
（1）∵ ，
∴，
∵，
∴是差解方程；
（2）∵ 关于的一元一次方程是差解方程，
∴
解得： ，
所以的值为．