题目内容
如图,已知△ABE≌△ACD,且AB=AC.
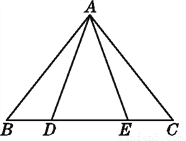
(1)说明△ABE经过怎样的变换后可与△ACD重合.
(2)∠BAD与∠CAE有何关系?请说明理由.
(3)BD与CE相等吗?为什么?
（1）见解析；（2）∠BAD=∠CAE；（3）相等
【解析】试题分析：（1）由几何变换的类型说明即可，
（2）由三角形全等的性质求解即可，
（3）由三角形全等的性质求解即可．
试题解析: (1)△ABE先水平翻转，再平移即可与△ACD重合；
(2)∠BAD=∠CAE.
∵△ABE≌△ACD，
∴∠BAE=∠CAD，
∴∠BAE?∠DAE=∠CAD?∠...
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
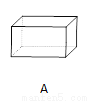
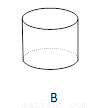
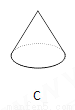
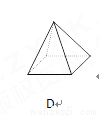
下面立体图形，从正面、左面、上面观察都不可能看到长方形的是( )
C
【解析】试题分析：A、主视图为长方形，左视图为长方形，俯视图为长方形，故本选项错误；
B、主视图为长方形，左视图为长方形，俯视图为圆，故本选项错误；
C、主视图为等腰三角形，左视图为等腰三角形，俯视图为圆，从正面、左面、上面观察都不可能看到长方形，故本选项正确；
D、主视图为三角形，左视图为三角形，俯视图为有对角线的矩形，故本选项错误．
故选：C． 如图，在△ABC中，DE是边AB的垂直平分线，BC=8cm，AC=5cm，则△ADC的周长为（ ）
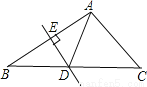
A. 14cm B. 13cm C. 11cm D. 9cm
B
【解析】试题解析：∵DE是边AB的垂直平分线
∴BD=AD
∴△ADC的周长为AC+DC+AD=AC+BC=5+8=13cm．
故选B. 已知，如图，四边形ABCD中．AB=AD，CB=CD，AC与BD交于点E．求证：（1）∠1=∠2；（2）AC⊥BD．
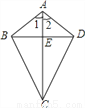
（1）证明见解析（2）证明见解析
【解析】试题分析：（1）由SSS证明△ABC≌△ADC，得出对应角相等即可；
（2）由线段垂直平分线的性质定理的逆定理得出点A在BD的垂直平分线上，点C在BD的垂直平分线上，得出AC垂直平分BD即可．
试题解析：（1）在△ABC和△ADC中，
，
∴△ABC≌△ADC（SSS），
∴∠1=∠2；
（2）∵AB=AD，CB=... 如图，AB=CD，AD=CB，那么下列结论中错误的是（ ）
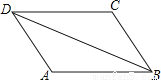
A. ∠A=∠C B. AB=AD C. AD∥BC D. AB∥CD
B
【解析】∵在△ABD和△CDB中，
，
∴△ABD≌△CDB，
∴∠ADB=∠CBD，∠ABD=∠CDB，∠A=∠C
∴AD∥BC，AB∥CD，
∴A、C、D选项正确.
故选：B. 如图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,指出其他的对应边和对应角.
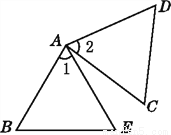
见解析
【解析】试题分析：先根据△ABE≌△ACD，可以确定点A的对应点是A，点B的对应点是C，点D的对应点是E，然后根据对应顶点，结合图形即可找出对应边和对应角.
试题解析：∵△ABE≌△ACD，∠1=∠2，∠B=∠C，
∴点A的对应点是A，点B的对应点是C，点E的对应点是D，
∴∠BAE与∠CAD是对应角，AB与AC，BE与CD，AD与AE是对应边. 如图,沿直线AC对折,△ABC与△ADC重合,则△ABC≌___________,AB的对应边是___________,∠BCA的对应角是___________.
△ADC AD ∠DCA
【解析】本题考查的是全等三角形的性质
根据全等三角形的对应边相等、对应角相等即可判断， 如图，∠A＝∠B，∠C＝α，DE⊥AC，FD⊥AB，则∠EDF等于( )
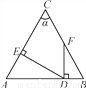
A. α B. 90°－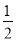
α C. 90°－α D. 180°－2α
B
【解析】∵∠A=∠B，∠C=α，
∴∠A=∠B=（180°-α），
∵DE⊥AC，FD⊥AB，
∴∠AED=∠FDB=90°，
∴∠ADE=90°-（180°-α）=α，
∴∠EDF =180°-90°-α=90°-α，
故选B． 某班黑板是一个长方形，它的面积为6a2－9ab＋3a，已知这个长方形的长为3a，则宽为_____.
2a-3b+1
【解析】由题意可得，长方形的宽为：（6a2－9ab＋3a）÷3a=2a-3b+1.