Question

1．如图，在给定的一张平行四边形纸片上作一个菱形．小米的作法是：连接AC，作AC的垂直平分线MN分别交AD，AC，BC于M，O，N，连接AN，CM，则四边形ANCM是菱形．则小米的依据是对角线互相垂直的平行四边形是菱形．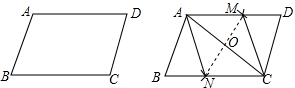

Answer 1

分析 先根据MN垂直平分AC，推导出△AOM≌△CON，进而的而出AM=CN，再根据AM∥CN，判定四边形AMCN是平行四边形，最后根据MN⊥AC，得出四边形AMCN是菱形．

解答 解：∵AC的垂直平分线MN分别交AD，AC，BC于M，O，N，
∴AO=CO，∠AOM=∠CON，
∵AD∥BC，
∴∠AMO=∠CNO，
在△AOM和△CON中
$\left\{\begin{array}{l}{∠AMO=∠CNO}\\{∠AOM=∠CON}\\{AO=CO}\end{array}\right.$
∴△AOM≌△CON（AAS）
∴AM=CN，
又∵AM∥CN，
∴四边形AMCN是平行四边形，
又∵MN⊥AC，
∴四边形AMCN是菱形．（对角线互相垂直的平行四边形是菱形）
故答案为：对角线互相垂直的平行四边形是菱形．

点评 本题主要考查了菱形的判定，对角线互相垂直的平行四边形是菱形，几何语言为：∵AC⊥BD，四边形ABCD是平行四边形，∴平行四边形ABCD是菱形．