题目内容
19.在Rt△ABC中,∠C=90°,a、b、c分别是∠A,∠B、∠C的对边,若关于x的方程c(x2+1)-2$\sqrt{2}$bx-a(x2-1)=0的两根平方和为10,求$\frac{b}{a}$的值.分析 将原方程整理为一元二次方程的一般形式,设方程两根为x1,x2,再根据两根平方和为10,列出等式并变形,将两根关系整体代入即可.
解答 解:原方程整理为(c-a)x2-2$\sqrt{2}$bx+(c+a)=0,
设x1,x2是方程的两个根,则x12+x22=10,即(x1+x2)2-2x1x2=10,
把方程根公式代入,得($\frac{2\sqrt{2}b}{c-a}$)2-2×$\frac{c+a}{c-a}$=10,即4b2-(c2-a2)=5(c-a)2,
由勾股定理得:c2-a2=b2,代入以上方程整理后有
3b2=5(c-a)2.
∵c是斜边,
∴c>a,两边开平方,得$\sqrt{3}$b+$\sqrt{5}$a=$\sqrt{5}$c,
两边同时平方得,
3b2+5a2+2$\sqrt{15}$ab=5c2,
再次将勾股定理代入得,
3b2+5a2+2$\sqrt{15}$ab=5a2+5b2,
2b2=2$\sqrt{15}$ab,
∴$\frac{b}{a}$=$\sqrt{15}$.
点评 本题考查了三角形的边角关系,根与系数关系,勾股定理的运用.关键是根据题意得出x12+x22=10,将等式变形,将根与系数关系代入,结合勾股定理求解.

练习册系列答案
相关题目
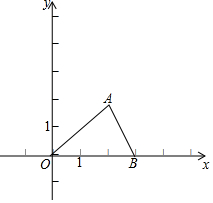 如图:A,B两点的坐标分别是(2,$\sqrt{3}$),(3,0).
如图:A,B两点的坐标分别是(2,$\sqrt{3}$),(3,0).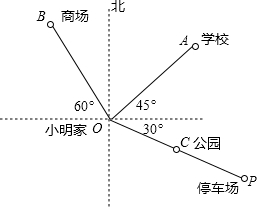 如图是小明家(图中点O)和学校所在地的简单地图,已知OA=2cm,OB=2.5cm,OP=4cm,C为OP的中点.
如图是小明家(图中点O)和学校所在地的简单地图,已知OA=2cm,OB=2.5cm,OP=4cm,C为OP的中点.