题目内容
11.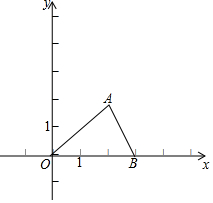 如图:A,B两点的坐标分别是(2,$\sqrt{3}$),(3,0).
如图:A,B两点的坐标分别是(2,$\sqrt{3}$),(3,0).(1)将△OAB向下平移$\sqrt{3}$个单位求所得的三角形的三个顶点的坐标;
(2)求△OAB的面积.
分析 (1)将△OAB向下平移${\sqrt{3}}_{\;}^{\;}$个单位,此时点A在x轴上;将△OAB各点的横坐标不变,纵坐标减去$\sqrt{3}$即可得到平移后的各点的坐标;
(2)△OAB的面积=OB×点A的纵坐标÷2,把相关数值代入即可求解.
解答 解:(1)
∴所得的三角形的三个顶点的坐标为A′(2,0),O′(0,-$\sqrt{3}$),B′(3,-$\sqrt{3}$);
(2)△OAB的面积=$\frac{1}{2}$×3×$\sqrt{3}$=$\frac{3\sqrt{3}}{2}$.
点评 此题考查了二次根式的应用及平移变化的知识,用到的知识点为:三角形的面积等于底与高积的一半;上下平移只改变点的纵坐标,上加下减.

练习册系列答案
相关题目
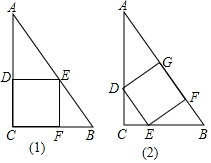 已知直角三角形的铁片ABC的两条直角边BC、AC的长分别为3、4,按图示所采用两种方法,各剪一块正方形的铁片,试比较哪一种方法剪出的正方形的面积较大.
已知直角三角形的铁片ABC的两条直角边BC、AC的长分别为3、4,按图示所采用两种方法,各剪一块正方形的铁片,试比较哪一种方法剪出的正方形的面积较大.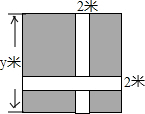 如图,小区在边长为y米的正方形内,修宽为2米的通道,其余部分种草.
如图,小区在边长为y米的正方形内,修宽为2米的通道,其余部分种草.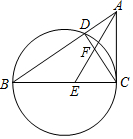 如图,△ABC中,以BC为直径的圆交AB于点D,∠ACD=∠ABC,E是BC上一点,AE与CD交于点F,若BE=6,tan∠ABC=$\frac{2}{3}$,tan∠AEC=$\frac{5}{3}$,则圆的直径是10,$\frac{AF}{FE}$=$\frac{10}{9}$.
如图,△ABC中,以BC为直径的圆交AB于点D,∠ACD=∠ABC,E是BC上一点,AE与CD交于点F,若BE=6,tan∠ABC=$\frac{2}{3}$,tan∠AEC=$\frac{5}{3}$,则圆的直径是10,$\frac{AF}{FE}$=$\frac{10}{9}$. 如图:正方形ABCD中,点E在AB上,点F在BC的延长线上,且AE=CF,DG⊥EF于H交BC于G.若tan∠BHG=$\frac{3}{4}$,△BGH的面积为3,求DK的长为5.
如图:正方形ABCD中,点E在AB上,点F在BC的延长线上,且AE=CF,DG⊥EF于H交BC于G.若tan∠BHG=$\frac{3}{4}$,△BGH的面积为3,求DK的长为5.