题目内容
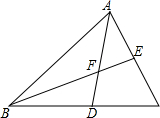
1．
如图，已知点D是BC上一点，△ABC∽△DBA，E，F分别是AC，AD的中点，且AB=28，BC=36，则BE：BF=9：7．
分析 根据相似三角形的性质：对应边上的中线的比等于相似比即可得到结论．
解答 解：∵E，F分别是AC，AD的中点，
∴BF，BE分别是AD，AC边上的中线，
∵△ABC∽△DBA，
∴$\frac{AB}{BC}=\frac{AD}{AC}=\frac{BF}{BE}$=$\frac{28}{36}$=$\frac{7}{9}$，
即：BE：BF=9：7．
故答案为：9：7．
点评 本题考查了相似三角形的性质，知道相似三角形对应边上的中线的比等于相似比是解题的关键．
练习册系列答案
活力课时同步练习册系列答案
相关题目
13．
如图是二次函数y=ax2+bx+c的图象，点P（a+b，bc）是坐标平面内的点，则点P在（ ）
如图是二次函数y=ax2+bx+c的图象，点P（a+b，bc）是坐标平面内的点，则点P在（ ）| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
如图所示，△ABC的角平分线AD，BE相交于点F，∠C=60°，求证：AB=AE+BD．