题目内容
8. 在不透明的箱子里放有4个乒乓球.每个乒乓球上分别写有数字1、2、3、4,从箱子中摸出一个球记下数字后放回箱中,摇匀后再摸出一个球记下数字.若将第一次摸出的球上的数字记为点的横坐标,第二次摸出的球上的数字记为点的纵坐标.
在不透明的箱子里放有4个乒乓球.每个乒乓球上分别写有数字1、2、3、4,从箱子中摸出一个球记下数字后放回箱中,摇匀后再摸出一个球记下数字.若将第一次摸出的球上的数字记为点的横坐标,第二次摸出的球上的数字记为点的纵坐标.(1)请用列表法或树状图法写出两次摸球后所有可能的结果;
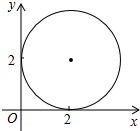
(2)求这样的点落在如图所示的圆中的概率(注:图中圆心在直角坐标系中的第一象限内,并且分别与x轴、y轴切于点(2,0)和(0,2)两点.
分析 (1)画树状图展示所有16种等可能的结果数;
(2)根据点与圆的位置关系的判定方法找出点落在圆中的结果数,然后根据概率公式求解.
解答 解:(1)画树状图为:
共有16种等可能的结果数;
(2)点落在圆中的有(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3),
所以点落在如图所示的圆中的概率=$\frac{9}{12}$=$\frac{3}{4}$.
点评 本题考查了列表法与树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.也考查了点与圆的位置关系.

练习册系列答案
相关题目
18. 2015年10月29日,党的十八届五种全会胜利闭幕,某中学七、八年级各选派10名选手参加“党的十八届五中全会知识竞赛”计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下,其中七年级代表队得6分、10分的选手人数分别为a,b.
2015年10月29日,党的十八届五种全会胜利闭幕,某中学七、八年级各选派10名选手参加“党的十八届五中全会知识竞赛”计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下,其中七年级代表队得6分、10分的选手人数分别为a,b.
(1)请依据图表中的数据,求a,b的值;
(2)直接写出表中的m=6,n=20%;
(3)有人说七年级的合格率、优秀率均高于八年级,所以七年级队成绩比八年级队好,但也有人说八年级队成绩比七年级队好.请你给出两条支持八年级队成绩好的理由.
 2015年10月29日,党的十八届五种全会胜利闭幕,某中学七、八年级各选派10名选手参加“党的十八届五中全会知识竞赛”计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下,其中七年级代表队得6分、10分的选手人数分别为a,b.
2015年10月29日,党的十八届五种全会胜利闭幕,某中学七、八年级各选派10名选手参加“党的十八届五中全会知识竞赛”计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下,其中七年级代表队得6分、10分的选手人数分别为a,b.| 队别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
| 七年级 | 6.7 | m | 3.41 | 90% | n |
| 八年级 | 7.1 | 7.5 | 1.69 | 80% | 10% |
(2)直接写出表中的m=6,n=20%;
(3)有人说七年级的合格率、优秀率均高于八年级,所以七年级队成绩比八年级队好,但也有人说八年级队成绩比七年级队好.请你给出两条支持八年级队成绩好的理由.
19.小晨和小冰两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)实验,他们共做了100次实验,实验的结果如下:
(1)计算“2点朝上”的频率和“3点朝上”的频率;
(2)小晨说:“根据实验,一次实验中出现4点朝上的概率是$\frac{1}{4}$;”小晨的这一说法正确吗?为什么?
(3)小冰说:“根据实验,如果掷1000次,那么出现5点朝上的次数是200次.”小冰的这一说法正确吗?为什么?
| 向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 出现次数 | 10 | 15 | 20 | 25 | 20 | 10 |
(2)小晨说:“根据实验,一次实验中出现4点朝上的概率是$\frac{1}{4}$;”小晨的这一说法正确吗?为什么?
(3)小冰说:“根据实验,如果掷1000次,那么出现5点朝上的次数是200次.”小冰的这一说法正确吗?为什么?
3.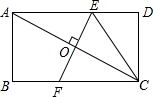 如图,将矩形纸片ABCD折叠,使得点A和点C重合,折痕是EF,连结EC.若AB=2,BC=4,则CE的长为( )
如图,将矩形纸片ABCD折叠,使得点A和点C重合,折痕是EF,连结EC.若AB=2,BC=4,则CE的长为( )
 如图,将矩形纸片ABCD折叠,使得点A和点C重合,折痕是EF,连结EC.若AB=2,BC=4,则CE的长为( )
如图,将矩形纸片ABCD折叠,使得点A和点C重合,折痕是EF,连结EC.若AB=2,BC=4,则CE的长为( )| A. | 3 | B. | 3.5 | C. | 2.5 | D. | 2.8 |
20.如图1,A、B、C是三个垃圾存放点,点B、C分别位于点A的正北和正东方向,AC=100米,四人分别测得∠C的度数如表:
他们又调查了各点的垃圾量,并绘制了下列尚不完整的统计图2,图3:
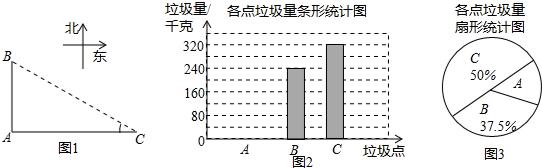
(1)求表中∠C度数的平均数$\overline{x}$;
(2)求A处的垃圾量,并将不完整的统计图2、3补充完整;
(3)用(1)中的$\overline{x}$作为∠C的度数,要将A处的垃圾沿道路AB都运到B处,已知运送1千克垃圾每米的费用为0.005元,求运垃圾所需的费用.
(注:sin37°=0.6,cos37°=0.8,tan37°=0.75)
| 甲 | 乙 | 丙 | 丁 | |
| ∠C(单位:度) | 34 | 36 | 38 | 40 |

(1)求表中∠C度数的平均数$\overline{x}$;
(2)求A处的垃圾量,并将不完整的统计图2、3补充完整;
(3)用(1)中的$\overline{x}$作为∠C的度数,要将A处的垃圾沿道路AB都运到B处,已知运送1千克垃圾每米的费用为0.005元,求运垃圾所需的费用.
(注:sin37°=0.6,cos37°=0.8,tan37°=0.75)
18.下列调查中,适合采用抽样调查的是( )
| A. | 对乘坐某班次飞机的乘客进行安检 | |
| B. | 了解一批节能灯管的使用寿命 | |
| C. | 选出某班学生中跑的最快的学生参加全县比赛 | |
| D. | 了解一班同学的视力情况 |
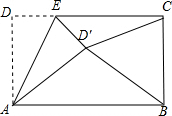 如图,矩形ABCD中,AD=5,AB=8,点E为DC上一个动点,把△ADE沿AE折叠,若点D的对应点D′,连接D′B和D′C,以下结论中:
如图,矩形ABCD中,AD=5,AB=8,点E为DC上一个动点,把△ADE沿AE折叠,若点D的对应点D′,连接D′B和D′C,以下结论中: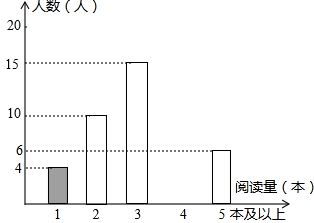 某学校为了解学生的课外阅读情况,王老师随机抽查部分学生,并对其暑假期间的课外阅读量进行统计分析,绘制成如图所示但不完整的统计图.已知抽查的学生在暑假期间阅读量为2本的人数占抽查总人数的20%,根据所给出信息,解答下列问题:
某学校为了解学生的课外阅读情况,王老师随机抽查部分学生,并对其暑假期间的课外阅读量进行统计分析,绘制成如图所示但不完整的统计图.已知抽查的学生在暑假期间阅读量为2本的人数占抽查总人数的20%,根据所给出信息,解答下列问题: