题目内容
3.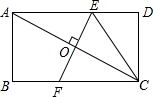 如图,将矩形纸片ABCD折叠,使得点A和点C重合,折痕是EF,连结EC.若AB=2,BC=4,则CE的长为( )
如图,将矩形纸片ABCD折叠,使得点A和点C重合,折痕是EF,连结EC.若AB=2,BC=4,则CE的长为( )| A. | 3 | B. | 3.5 | C. | 2.5 | D. | 2.8 |
分析 由四边形ABCD是矩形,得到CD=AB=2,AD=BC=4,∠D=90°,根据折叠的性质得到AE=CE,根据勾股定理列方程即可得到结论.
解答 解:∵四边形ABCD是矩形,
∴CD=AB=2,AD=BC=4,∠D=90°,
∵将矩形纸片ABCD折叠,使得点A和点C重合,
∴AE=CE,
∴DE=AD-AE=4-CE,
∵CE2=DE2+CD2,
即CE2=(4-CE)2+22,
∴CE=2.5,
故选C.
点评 该题主要考查了翻折变换的性质及其应用问题,矩形的性质,灵活运用翻折变换的性质、勾股定理等几何知识点来分析、判断、推理或解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
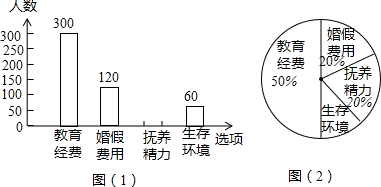
 某教学学习小组对“人们了解国家大事的途径”进行调查.
某教学学习小组对“人们了解国家大事的途径”进行调查.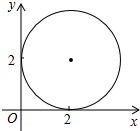 在不透明的箱子里放有4个乒乓球.每个乒乓球上分别写有数字1、2、3、4,从箱子中摸出一个球记下数字后放回箱中,摇匀后再摸出一个球记下数字.若将第一次摸出的球上的数字记为点的横坐标,第二次摸出的球上的数字记为点的纵坐标.
在不透明的箱子里放有4个乒乓球.每个乒乓球上分别写有数字1、2、3、4,从箱子中摸出一个球记下数字后放回箱中,摇匀后再摸出一个球记下数字.若将第一次摸出的球上的数字记为点的横坐标,第二次摸出的球上的数字记为点的纵坐标.