题目内容
在□ABCD中，∠B＝100°，则∠A，∠D的度数分别是（ ）
A. ∠A＝80°，∠D＝80° B. ∠A＝80°，∠D＝100°
C. ∠A＝100°，∠D＝80° D. ∠A＝100°，∠D＝100°
B
【解析】∵在□ABCD中，∠B＝100°，
∴∠A=180°-∠B=180°-100°=80°， ∠D=∠B=100°.
故选B.
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
如果分式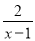
与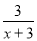
的值相等，则
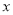的值是( )
A. 9 B. 7 C. 5 D. 3
A
【解析】由题意得：
故选A. 对于分式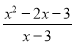
，当x=__时，分式无意义；当x=__时，分式值为零．
3, -1
【解析】当x-3=0时，分式无意义,
解之得
x=3;
当 时，分式值为零，
解之得
x=-1. 如图，已知AB∥CD，则x的度数是____________.
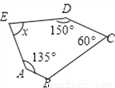
75º
【解析】∵AB∥CD，
∴∠B=180°-60°=120°，
∵多边形ABCDE是五边形，
∴∠A+∠B+∠C+∠D+∠E=(5-2)×180°=540°，
∴∠E=540°-∠A-∠B-∠C-∠D=540°-135°-120°-60°-150°=75°． 如图，E是平行四边形内任一点，若S□ABCD=8，则图中阴影部分的面积是（ ）
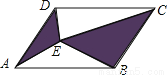
A. 3 B. 4 C. 5 D. 6
B
【解析】设两个阴影部分三角形的底为AD,CB,高分别为h1,h2,则h1+h2为平行四边形的高,
=4.
所以B选项是正确的. 解方程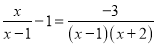
【解析】分析：观察可得最简公分母是(x-1）(x+2),方程两边乘最简公分母,可以把分式方程转化为整式方程求解；
本题解析：两边同时乘最简公分母
化成整式方程为：
整理得到： ，经检验是方程的解. 关于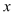
的分式方程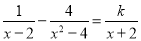
有增根x=—2，那么k=________________
1
【解析】分式方程去分母得：x+2?4=k(x?2)，
由增根为x=?2，代入整式方程得：?2+2?4=?4k，
解得：k=1.
故答案为：1. 先化简，再求值：(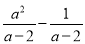
)÷
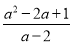，其中a＝3.
2
【解析】试题分析：本题考查了分式的化简求值，先把括号里按照同分母分式的加减法化简，然后把除法转化为乘法，并把分子分母分解因式约分，最后代入求值即可.
【解析】
()÷
=÷
=×
=×
=，
当a＝3时，
原式===2. 在等腰△ABC中，AB=AC，其周长为20cm，则AB边的取值范围是（ ）
A. 1cm＜AB＜4cm B. 5cm＜AB＜10cm
C. 4cm＜AB＜8cm D. 4cm＜AB＜10cm
B
【解析】试题分析：∵在等腰△ABC中，AB=AC，其周长为20cm，∴设AB="AC=x" cm，则BC=（20﹣2x）cm，∴，解得5cm＜x＜10cm．故选B．