��Ŀ����
3����ͼ����ABC�ڽ��ڡ�O����AB=AC����1����O����AE����BC��D����֤��AB•AC=AD•AE��
��2���ڣ�1���������µ���AE���ӳ�����BC���ӳ����ཻ�ڵ�Dʱ�����������Ƿ������������������֤����������������˵�����ɣ�
��3����֪��O �İ뾶2����ACB=40�㣬��BA�ij�����sin40���0.64��cos40���0.77��tan40���0.84�������ȷ��0.1��
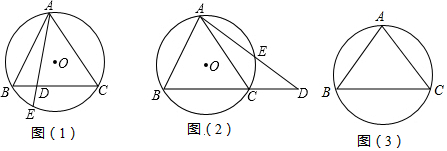
���� ��1����ͼ1�У�����CE��ֻҪ֤����AEC�ס�ACD�����ɽ�����⣻
��2����ͼ2�У�����BE��ֻҪ֤����AEB�ס�ABD�����ɽ�����⣻
��3����ͼ3�У���A����O��ֱ��AM������BM����Rt��ABM�У���ֱ�������μ��ɣ�
��� ��1��֤������ͼ1�У�����CE��
��AB=AC��
��$\widehat{AB}$=$\widehat{AC}$��
���AEC=��ACD��
�֡ߡ�EAC=��DAC��
���AEC�ס�ACD��
��$\frac{AE}{AC}$=$\frac{AC}{AD}$����AC2=AD•AE��
�֡�AB=AC��
��AB•AC=AD•AE��
��2�������������Գ�����
֤������ͼ2�У�����BE��
��AB=AC��
��$\widehat{AB}$=$\widehat{AC}$��
���AEB=��ABD��
�֡ߡ�EAB=��DAB
���AEB�ס�ABD��
��$\frac{AE}{AB}$=$\frac{AB}{AD}$����AB2=AD•AE��
�֡�AB=AC��
��AB•AC=AD•AE��
��3���⣺��ͼ3�У���A����O��ֱ��AM������BM��
���ABM=90�㣬
�ߡ�AMB=��ACB=40�㣬
��Rt��ABD��AM=4��
��sin��AMB=$\frac{AB}{AM}$��
��AB=4sin40��=4��0.64��2.6��
���� ���⿼��Բ�ۺ��⡢Բ�ܽǶ��������������ε��ж������ʡ�������Ǻ�����֪ʶ������Ĺؼ���ѧ�����ӳ��ø����ߣ��������������ν�����⣬�����п��������ͣ�

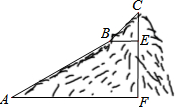 ��ͼ��Ϊ����һ��ɽ��CF�ĸ߶ȣ�����ɽ��ij��ɽ�»���ΪAB��BC���Σ�ÿһ��ɽ�½����ǡ�ֱ���ģ�����³�AB=800�ף�BC=200�ף�б��AB���¶�i=1��2�����ǡ�CBE=50�㣬��ɽ��ĸ߶�CFԼΪ���������ף������õIJο����ݣ�sin50���0.8��tan50���1.2��$\sqrt{5}$��2.24��
��ͼ��Ϊ����һ��ɽ��CF�ĸ߶ȣ�����ɽ��ij��ɽ�»���ΪAB��BC���Σ�ÿһ��ɽ�½����ǡ�ֱ���ģ�����³�AB=800�ף�BC=200�ף�б��AB���¶�i=1��2�����ǡ�CBE=50�㣬��ɽ��ĸ߶�CFԼΪ���������ף������õIJο����ݣ�sin50���0.8��tan50���1.2��$\sqrt{5}$��2.24��| A�� | 500 | B�� | 516 | C�� | 530 | D�� | 580 |
| A�� | ��-2��3�� | B�� | ��1��-6�� | C�� | ��-3��-2�� | D�� | ��3��3�� |
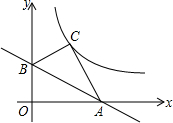 ��ͼ����֪��A��6��0����B��0��2$\sqrt{3}$����OΪ����ԭ�㣬��O����ֱ��AB�ĶԳƵ�Cǡ�����ڷ���������y=$\frac{k}{x}$��k��0����ͼ���ϣ���k��ֵ��
��ͼ����֪��A��6��0����B��0��2$\sqrt{3}$����OΪ����ԭ�㣬��O����ֱ��AB�ĶԳƵ�Cǡ�����ڷ���������y=$\frac{k}{x}$��k��0����ͼ���ϣ���k��ֵ��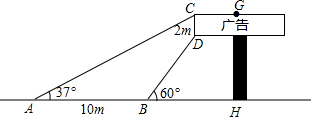 ��ͼ�������ι���Ƽ���¥����������֪CD=2m���������õ���CAH=37�㣬��DBH=60�㣬AB=10m����GH�ij������ο����ݣ�tan37���0.75��$\sqrt{3}$��1.732�������ȷ��0.1m��
��ͼ�������ι���Ƽ���¥����������֪CD=2m���������õ���CAH=37�㣬��DBH=60�㣬AB=10m����GH�ij������ο����ݣ�tan37���0.75��$\sqrt{3}$��1.732�������ȷ��0.1m��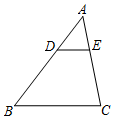 ��ͼ���ڡ�ABC�У�DΪAB����һ�㣬DE��BC��AC�ڵ�E�����$\frac{AE}{EC}$=$\frac{1}{2}$��DE=7����ôBC�ij�Ϊ21��
��ͼ���ڡ�ABC�У�DΪAB����һ�㣬DE��BC��AC�ڵ�E�����$\frac{AE}{EC}$=$\frac{1}{2}$��DE=7����ôBC�ij�Ϊ21�� ��ͼ���ڡ�O���ڽ������ABCDE�У���B+��E=215�㣬���CAD=35�㣮
��ͼ���ڡ�O���ڽ������ABCDE�У���B+��E=215�㣬���CAD=35�㣮