题目内容
13.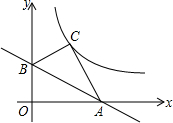 如图,已知点A(6,0),B(0,2$\sqrt{3}$),O为坐标原点,点O关于直线AB的对称点C恰好落在反比例函数y=$\frac{k}{x}$(k>0)的图象上,求k的值.
如图,已知点A(6,0),B(0,2$\sqrt{3}$),O为坐标原点,点O关于直线AB的对称点C恰好落在反比例函数y=$\frac{k}{x}$(k>0)的图象上,求k的值.
分析 先连接OC,在Rt△AOB中,利用三角函数得出∠BAO,再由对称性得出∠AOC,得出△AOC是等边三角形,过点C作CF⊥AO于F点,利用三角函数得出CF,即可得出点C的坐标,再求k的值即可.
解答  解:∵点A(6,0),B(0,$2\sqrt{3}$),
解:∵点A(6,0),B(0,$2\sqrt{3}$),
∴OA=6,OB=$2\sqrt{3}$.
在Rt△AOB中,tan∠BAO=$\frac{OB}{OA}=\frac{{\sqrt{3}}}{3}$,
∴∠BAO=30°,
连接OC,
∵点O关于直线AB的对称点是C,
∴OC⊥AB,则∠AOC=60°,
∴△AOC为等边三角形,且AO=CO=6,
过点C作CF⊥AO于F点,
则OF=$\frac{1}{2}$OA=3,CF=OC•sin∠FOC=$3\sqrt{3}$,
则点C的坐标为(3,$3\sqrt{3}$)
∵C在反比例函数$y=\frac{k}{x}(k>0)$的图象上,
∴$k=3×3\sqrt{3}=9\sqrt{3}$.
点评 本题考查了反比例函数图象上点的坐标特征,本题是一道综合性的题目,涉及到的知识点有三角函数、对称以及用待定系数法求反比例函数的解析式,难度中等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 甲乙两人同时登西山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图11所示,乙在A处提速后的速度是甲登山速度的3.根据图象所提供的信息解答下列问题中正确的个数为( )
甲乙两人同时登西山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图11所示,乙在A处提速后的速度是甲登山速度的3.根据图象所提供的信息解答下列问题中正确的个数为( )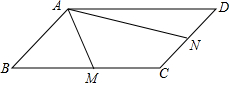 如图,在平行四边形ABCD中,M、N分别为BC、CD的中点,AM=1,AN=2,∠MAN=60°,则AB的长为$\frac{4}{3}$.
如图,在平行四边形ABCD中,M、N分别为BC、CD的中点,AM=1,AN=2,∠MAN=60°,则AB的长为$\frac{4}{3}$.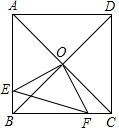 如图,已知正方形ABCD的对角线交于点O,过O点作OE⊥OF,分别交AB、BC于E、F,若AE=4,CF=3,则EF等于5.
如图,已知正方形ABCD的对角线交于点O,过O点作OE⊥OF,分别交AB、BC于E、F,若AE=4,CF=3,则EF等于5.