题目内容
1.已知$\sqrt{x}$+$\frac{1}{\sqrt{x}}$=2,求$\sqrt{\frac{x}{{x}^{2}+7x+1}}$-$\sqrt{\frac{x}{{x}^{2}+14x+1}}$的值.分析 先把已知条件两边平方可得x+$\frac{1}{x}$=2,再把$\frac{x}{{x}^{2}+7x+1}$和$\frac{x}{{x}^{2}+14x+1}$的分子分母都除以x后利用整体代入计算出它们的值,然后利用算术平方根的定义计算原式的值.
解答 解:∵$\sqrt{x}$+$\frac{1}{\sqrt{x}}$=2,
∴x+$\frac{1}{x}$=2,
∴$\frac{x}{{x}^{2}+7x+1}$=$\frac{1}{x+7+\frac{1}{x}}$=$\frac{1}{2+7}$=$\frac{1}{9}$,$\frac{x}{{x}^{2}+14x+1}$=$\frac{1}{x+14+\frac{1}{x}}$=$\frac{1}{2+14}$=$\frac{1}{16}$,
∴原式=$\sqrt{\frac{1}{9}}$+$\sqrt{\frac{1}{16}}$
=$\frac{1}{3}$+$\frac{1}{4}$
=$\frac{7}{12}$.
点评 本题考查了二次根式的化简求值:二次根式的化简求值,一定要先化简再代入求值.二次根式运算的最后,注意结果要化到最简二次根式,二次根式的乘除运算要与加减运算区分,避免互相干扰.也考查了代数式的变形能力.

练习册系列答案
相关题目
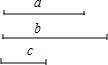 已知:线段a、b、c,如图所示,求作:线段x,使2a:b=3c:x.
已知:线段a、b、c,如图所示,求作:线段x,使2a:b=3c:x.