题目内容
12.计算:$\frac{1}{2}$+($\frac{1}{3}$+$\frac{2}{3}$)+($\frac{1}{4}$+$\frac{2}{4}$+$\frac{3}{4}$)+($\frac{1}{5}$+$\frac{2}{5}$+$\frac{3}{5}$+$\frac{4}{5}$)+…+($\frac{1}{60}$+$\frac{2}{60}$+…+$\frac{59}{60}$)分析 通过计算可知$\frac{1}{3}$+$\frac{2}{3}$=1,$\frac{1}{4}$+$\frac{2}{4}$+$\frac{3}{4}$=$\frac{3}{2}$,$\frac{1}{5}$+$\frac{2}{5}$+$\frac{3}{5}$+$\frac{4}{5}$=2,$\frac{1}{60}$+$\frac{2}{60}$+…+$\frac{59}{60}$=$\frac{59}{2}$,然后将首项和尾项相加,其结果×59÷2即可.
解答 解:原式=$\frac{1}{2}$+1+$\frac{3}{2}$+2+…+$\frac{59}{2}$
=($\frac{1}{2}+\frac{59}{2}$)×59÷2
=885.
点评 本题主要考查的是有理数的加法,掌握高斯求和公式是解题的关键.

练习册系列答案
相关题目
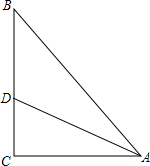 在Rt△ABC中,∠C=90°,tan∠CAD=$\frac{\sqrt{3}}{3}$,AB=14,AD=10,求BD的长.
在Rt△ABC中,∠C=90°,tan∠CAD=$\frac{\sqrt{3}}{3}$,AB=14,AD=10,求BD的长.