题目内容
9.在同一直角坐标系中作出二次函数y=-x2,y=-0.5x2的图象,然后回答下列问题:(1)它们的开口方向、对称轴和顶点坐标分别是什么?
(2)请描述一下在对称轴的左侧函数值的变化情况.
分析 根据二次函数的性质,由开口方向、对称轴、顶点坐标作出函数图象.
(1)根据画出的函数图象并结合其性质即可求解;
(2)结合函数图象,根据二次函数的性质即可求解.
解答 解:在同一直角坐标系中作出作出二次函数y=-x2,y=-0.5x2的图象如下所示: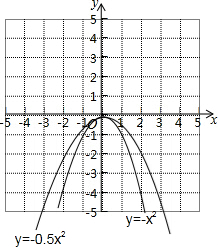
(1)抛物线y=-x2的开口方向是向下,对称轴是y轴,顶点坐标是(0,0);二次函数y=一$\frac{1}{2}$x2的开口方向是向下,对称轴是y轴,顶点坐标是(0,0);
(2)在对称轴的左侧函数值随x的增大而增大.
点评 本题结合图象考查了二次函数的性质,重点是注意函数的开口方向、顶点坐标、对称轴及单调性与最值的问题.

练习册系列答案
相关题目
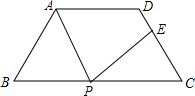 如图,在等腰梯形ABCD中,AD∥BC,AD=6cm,BC=14cm,∠B=60°,P为下底BC上一点(不与点B、C重合),连接AP,过点P作射线PE交线段DC于点E,使得∠APE=∠B,若DE:EC=5:3,则BP=2cm或12cm.
如图,在等腰梯形ABCD中,AD∥BC,AD=6cm,BC=14cm,∠B=60°,P为下底BC上一点(不与点B、C重合),连接AP,过点P作射线PE交线段DC于点E,使得∠APE=∠B,若DE:EC=5:3,则BP=2cm或12cm.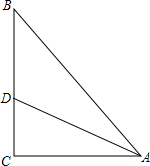 在Rt△ABC中,∠C=90°,tan∠CAD=$\frac{\sqrt{3}}{3}$,AB=14,AD=10,求BD的长.
在Rt△ABC中,∠C=90°,tan∠CAD=$\frac{\sqrt{3}}{3}$,AB=14,AD=10,求BD的长.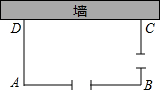 矩形自行车场地ABCD一边靠墙(墙长10m),在AB和BC边各开一个1米宽的校门(不用木板),现有能围成14m长的木板,当AD长为多少时,自行车场地的面积最大?最大面积是多少.
矩形自行车场地ABCD一边靠墙(墙长10m),在AB和BC边各开一个1米宽的校门(不用木板),现有能围成14m长的木板,当AD长为多少时,自行车场地的面积最大?最大面积是多少.