题目内容
10.已知:直线l:y=x+2与过点(0,-2),且与平行于x轴的直线交于点A,点A关于直线x=-1的对称点为点B.(1)求A,B两点的坐标;
(2)若抛物线y=-x2+bx+c经过A,B两点,求抛物线解析式;
(3)若抛物线y=-x2+bx+c的顶点在直线l上移动,当抛物线与线段AB有一个公共点时,求抛物线顶点横坐标t的取值范围.
分析 (1)由点A在直线l上可得A的坐标,根据点A、B关于直线x=-1对称可得点B坐标;
(2)根据(1)中A、B两点坐标,利用待定系数法可求得解析式;
(3)由顶点在直线l上可设顶点坐标为(t,t+2),继而可得抛物线解析式为y=-(x-t)2+t+2,根据抛物线与线段AB有一个公共点,考虑抛物线过点A或点B临界情况可得t的范围.
解答 解:(1)由题可知A点的纵坐标为-2,
∵点A在直线l:y=x+2上,
∴A(-4,-2),
由对称性可知B(2,-2);
(2)∵抛物线y=-x2+bx+c过点A、B,
∴$\left\{\begin{array}{l}{-16-4b+c=-2}\\{-4+2b+c=-2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=-2}\\{c=6}\end{array}\right.$,
∴抛物线解析式为y=-x2-2x+6;
(3)∵抛物线y=-x2+bx+c顶点在直线y=x+2上,
由题可知,设抛物线顶点坐标为(t,t+2),
∴抛物线解析式可化为y=-(x-t)2+t+2.
把A(-4,-2)代入解析式可得-2=-(-4-t)2+t+2,
解得:t=-3或t=-4.
∴-4≤t<-3,
把B(2,-2)代入解析式可得-2=-(2-t)2+t+2.
解得:t=0或t=5,
∴0<t≤5.
综上可知t的取值范围时-4≤t<-3或0<t≤5.
点评 本题考查待定系数法求二次函数解析式及二次函数的图象与性质,待定系数求解析式是解题的根本、前提,将抛物线与线段AB有一个公共点转化为方程问题是解题关键.

练习册系列答案
相关题目
20.下列命题为真命题的是( )
| A. | 平分弦的直径垂直于弦 | |
| B. | 在同圆或等圆中、相等的弦所对的圆周角相等 | |
| C. | 平分弦所对的一条弧的直径一定垂直平分这条弦 | |
| D. | 相等的圆心角所对的弧相等,所对的弦也相等 |
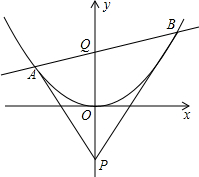 已知抛物线y=ax2,点P、Q为抛物线对称轴上两点,且P、Q关于抛物线顶点对称,过Q点任意作一条直线与抛物线交于A、B两点,求证:抛物线对称轴平分∠APB.
已知抛物线y=ax2,点P、Q为抛物线对称轴上两点,且P、Q关于抛物线顶点对称,过Q点任意作一条直线与抛物线交于A、B两点,求证:抛物线对称轴平分∠APB.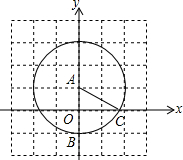 如图,已知点A(0,1),B(0,-1),以点A为圆心,AB为半径作圆,交x轴的正半轴于点C,则tan∠BAC=$\sqrt{3}$.
如图,已知点A(0,1),B(0,-1),以点A为圆心,AB为半径作圆,交x轴的正半轴于点C,则tan∠BAC=$\sqrt{3}$.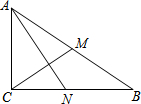 如图,Rt△ABC中,∠ACB=90°,CM为AB边上的中线,AN⊥CM,交BC于点N.若CM=3,AN=4,则tan∠CAN的值为$\frac{2}{3}$.
如图,Rt△ABC中,∠ACB=90°,CM为AB边上的中线,AN⊥CM,交BC于点N.若CM=3,AN=4,则tan∠CAN的值为$\frac{2}{3}$.