题目内容
20.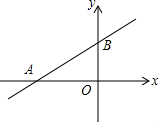 如图,直线y=$\frac{3}{4}x+3$与x、y轴分别交于A、B两点,则cos∠BAO的值是( )
如图,直线y=$\frac{3}{4}x+3$与x、y轴分别交于A、B两点,则cos∠BAO的值是( )| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{5}{4}$ |
分析 根据一次函数图象上点的坐标特征求出点A、B的坐标,得到OA、OB的长,根据勾股定理求出AB,根据余弦的定义解答即可.
解答 解:当x=0时,y=3,
当y=0时,x=-4,
∴直线y=$\frac{3}{4}x+3$与x、y轴的交点A的坐标(-4,0)、B(0,3),
∴OA=4,OB=3,
由勾股定理得,AB=5,
则cos∠BAO=$\frac{OA}{AB}$=$\frac{4}{5}$,
故选:A.
点评 本题考查的是锐角三角函数的定义,掌握在直角三角形中,一个锐角的对边比斜边是这个角的正弦,邻边比斜边是这个角的余弦,对边比邻边是这个角的正切是解题的关键.

练习册系列答案
相关题目
10.下列运算正确的是( )
| A. | x2•x3=x6 | B. | (x2)3=x6 | C. | x2+x3=x5 | D. | x2+x2=2x4 |
11. 如图,E是正方形ABCD的边BC延长线上一点,且CE=AC,则∠E=( )
如图,E是正方形ABCD的边BC延长线上一点,且CE=AC,则∠E=( )
 如图,E是正方形ABCD的边BC延长线上一点,且CE=AC,则∠E=( )
如图,E是正方形ABCD的边BC延长线上一点,且CE=AC,则∠E=( )| A. | 90° | B. | 45° | C. | 30° | D. | 22.5° |
12.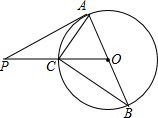 如图,AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C,连结AC、BC.若∠BAC=2∠BCO,AC=3,则PA的长为( )
如图,AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C,连结AC、BC.若∠BAC=2∠BCO,AC=3,则PA的长为( )
 如图,AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C,连结AC、BC.若∠BAC=2∠BCO,AC=3,则PA的长为( )
如图,AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C,连结AC、BC.若∠BAC=2∠BCO,AC=3,则PA的长为( )| A. | 3$\sqrt{3}$ | B. | 4 | C. | 5 | D. | 6 |