题目内容
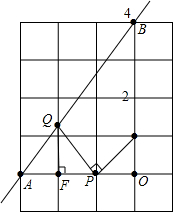 如图,直线y=
如图,直线y=| 4 |
| 3 |
(1)当t=2时,AP=
(2)证明:△QFP∽△POE;
(3)请表示出Q,E的坐标,并写出过程;
(4)在运动过程中,是否存在t使得以点B,Q,E为顶点的三角形与△ABO相似?若存在请求出t的值;若不存在,请说明理由.
考点:相似形综合题
专题:
分析:(1)由y=
x+4可求得AO=3,BO=4,所以当t=2时,可求出AP=AO-PO=3-2=1,而AQ=4,由条件可知QF∥BO,所以可知
=
,代入可求得QF;
(2)由QP⊥PE,PF⊥AO,可得∠QPF=∠PEO,结合直角可证明相似;
(3)由sin∠BAO=
=
=
,且AQ=2t,代入可表示出QF,进一步可求得AF,则可表示出Q点的坐标,再利用(2)中的相似可得
=
,代入可表示出E点的坐标;
(4)因为△ABO为直角三角形,所以BQE也为直角三角形,有两种情况即Q为直角顶点和E为直角顶点,利用对应边的比相等代入求t即可.
| 4 |
| 3 |
| AQ |
| AB |
| QF |
| OB |
(2)由QP⊥PE,PF⊥AO,可得∠QPF=∠PEO,结合直角可证明相似;
(3)由sin∠BAO=
| BO |
| AB |
| QF |
| AQ |
| 4 |
| 5 |
| QF |
| PO |
| PF |
| EO |
(4)因为△ABO为直角三角形,所以BQE也为直角三角形,有两种情况即Q为直角顶点和E为直角顶点,利用对应边的比相等代入求t即可.
解答:(1)解:由y=
x+4可求得AO=3,BO=4,由勾股定理可得AB=5,
当t=2时,则有AP=AO-PO=3-2=1,而AQ=4,
由条件可知QF∥BO,
所以
=
,
所以
=
,
解得QF=
,
故答案为:1;
;
(2)证明:
∵QP⊥PE,PF⊥AO,
∴∠PFP=∠POE,
且∠FPQ+∠EPO=∠PEO+∠EPO=90°,
∴∠QPF=∠PEO,
∴△QFP∽△POE;
(3)解:
在Rt△ABO和Rt△AQF中,sin∠BAO=
=
=
,且AQ=2t,
∴
=
,
∴QF=
,
∵
=
=tan∠BAO,
∴
=
,
∴AF=
,且AO=3,
∴OF=AO-AF=3-
,
∴Q点的坐标为(
-3,
),
由△QFP∽△POE可得
=
,
∵PO=t,∴PF=OF-PO=3-
-t=3-
,
∴
=
,
∴OE=
,
∴E点坐标为(0,
);
(4)解:
假设存在满足条件的t,分两种情况:
①当Q为直角顶点时,则有
=
,
由(3)可知BE=4-OE=4-
=
,BQ=AB-AQ=5-2t,
代入可得:
=
,
可解得t=
,
而由题意,当Q到达B点时的时间为t=
=2.5,即0≤t≤2.5,而
>2.5,故该种情况符合条件的t不存在;
②当E为直角顶点时,则有
=
,同样代入可得:
=
,解得t=
>2.5,故也不符合条件;
综上可知不存在使以点B,Q,E为顶点的三角形与△ABO相似的t的值.
| 4 |
| 3 |
当t=2时,则有AP=AO-PO=3-2=1,而AQ=4,
由条件可知QF∥BO,
所以
| AQ |
| AB |
| QF |
| OB |
所以
| 4 |
| 5 |
| QF |
| 4 |
解得QF=
| 16 |
| 5 |
故答案为:1;
| 16 |
| 5 |
(2)证明:
∵QP⊥PE,PF⊥AO,
∴∠PFP=∠POE,
且∠FPQ+∠EPO=∠PEO+∠EPO=90°,
∴∠QPF=∠PEO,
∴△QFP∽△POE;
(3)解:
在Rt△ABO和Rt△AQF中,sin∠BAO=
| BO |
| AB |
| QF |
| AQ |
| 4 |
| 5 |
∴
| QF |
| 2t |
| 4 |
| 5 |
∴QF=
| 8t |
| 5 |
∵
| QF |
| AF |
| BO |
| AO |
∴
| ||
| AF |
| 4 |
| 3 |
∴AF=
| 6t |
| 5 |
∴OF=AO-AF=3-
| 6t |
| 5 |
∴Q点的坐标为(
| 6t |
| 5 |
| 8t |
| 5 |
由△QFP∽△POE可得
| QF |
| PO |
| PF |
| OE |
∵PO=t,∴PF=OF-PO=3-
| 6t |
| 5 |
| 11t |
| 5 |
∴
| ||
| t |
3-
| ||
| OE |
∴OE=
| 15-11t |
| 8 |
∴E点坐标为(0,
| 15-11t |
| 8 |
(4)解:
假设存在满足条件的t,分两种情况:
①当Q为直角顶点时,则有
| BQ |
| BO |
| BE |
| BA |
由(3)可知BE=4-OE=4-
| 15-11t |
| 8 |
| 17-11t |
| 8 |
代入可得:
| 5-2t |
| 4 |
| ||
| 5 |
可解得t=
| 11 |
| 3 |
而由题意,当Q到达B点时的时间为t=
| 5 |
| 2 |
| 11 |
| 3 |
②当E为直角顶点时,则有
| BQ |
| BA |
| BE |
| BO |
| 5-2t |
| 5 |
| ||
| 4 |
| 25 |
| 3 |
综上可知不存在使以点B,Q,E为顶点的三角形与△ABO相似的t的值.
点评:本题主要考查相似三角形的判定和性质的综合应用,注意用t表示出线段长度则可化动为静,再利用相似即可找到线段之间的关系,代入可解决.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
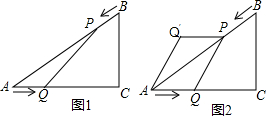 如图1,已知△ABC中,AB=10cm,AC=8cm,BC=6cm.如果点P由B出发沿BA方向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s.连接PQ,设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:
如图1,已知△ABC中,AB=10cm,AC=8cm,BC=6cm.如果点P由B出发沿BA方向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s.连接PQ,设运动的时间为t(单位:s)(0≤t≤4).解答下列问题: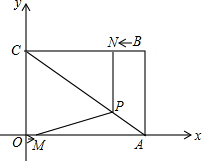 如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(6,0),(6,8).动点M、N分别从O、B同时出发,都以每秒1个单位的速度运动,其中点M沿OA向终点A运动,点N沿BC向终点C运动,过点N作NP⊥BC,交AC于点P,连接MP,已知动点运动了t秒.
如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(6,0),(6,8).动点M、N分别从O、B同时出发,都以每秒1个单位的速度运动,其中点M沿OA向终点A运动,点N沿BC向终点C运动,过点N作NP⊥BC,交AC于点P,连接MP,已知动点运动了t秒.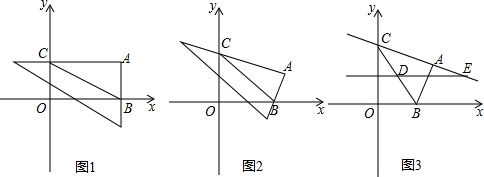

 如图,在△ABC中,∠A=150°,AB=AC=6cm,求△ABC的面积.
如图,在△ABC中,∠A=150°,AB=AC=6cm,求△ABC的面积.