��Ŀ����
��һ���㹻��������ΰ壬��ֱ�Ƕ�����ڵ�A��3��2������ֱ�DZ߷ֱ�x�ᡢy���ڵ�B��C����B��t��0����
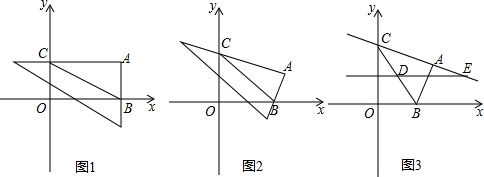
��1����ͼ1����t=3ʱ�����߶�BC�ij���
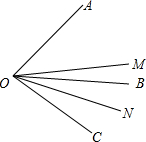
��2����ͼ2����B��C�ֱ���x�ᣬy����������ϣ����BOC�����ΪS������S����t�ĺ�����ϵʽ�������S�����ֵ��
��3��ȡBC���е�D������D��y��Ĵ�����ֱ��AC���ڵ�E����CDE�ܷ��Ϊ���������Σ����ܣ��������B�����ꣻ�����ܣ���˵�����ɣ�

��1����ͼ1����t=3ʱ�����߶�BC�ij���
��2����ͼ2����B��C�ֱ���x�ᣬy����������ϣ����BOC�����ΪS������S����t�ĺ�����ϵʽ�������S�����ֵ��
��3��ȡBC���е�D������D��y��Ĵ�����ֱ��AC���ڵ�E����CDE�ܷ��Ϊ���������Σ����ܣ��������B�����ꣻ�����ܣ���˵�����ɣ�
���㣺�������ۺ���
ר�⣺
��������1�����������ľ��빫ʽ���BC�ij��ȼ��ɣ�
��2����ͼ2����A��AH��x����H��AP��y����P���������������Σ���ABH�ס�ACP���������������εĶ�Ӧ�߳ɱ������CP�ij��ȣ���OC=OP+CP��Ȼ���������ε������ʽ���н�ɣ�
��3����Ҫ�������ۣ��ٵ�0��t��3ʱ������E���A�غ�ʱ����CDEΪ���������Σ���ֱ��DE������A��
�ڵ�3��t��
ʱ����CD=CE����A��AM��y�ᣬ�������������Σ���AMC�ס�DHC���������������ε���������t��ֵ��
�۵�t��
ʱ����CEDΪ�۽ǣ���CE=DE����֤��OCF�ա�ABF�����ȫ�������εĶ�Ӧ����ȣ������ù��ɶ����г�����t�ķ��̣�ͨ���ⷽ������t��ֵ��
����ͼ5����t��0ʱ�����õ��������ε����ʽ��н��
��2����ͼ2����A��AH��x����H��AP��y����P���������������Σ���ABH�ס�ACP���������������εĶ�Ӧ�߳ɱ������CP�ij��ȣ���OC=OP+CP��Ȼ���������ε������ʽ���н�ɣ�
��3����Ҫ�������ۣ��ٵ�0��t��3ʱ������E���A�غ�ʱ����CDEΪ���������Σ���ֱ��DE������A��
�ڵ�3��t��
| 13 |
| 3 |
�۵�t��
| 13 |
| 3 |
����ͼ5����t��0ʱ�����õ��������ε����ʽ��н��
��� ��1���ߵ�A��3��2����
��1���ߵ�A��3��2����
��AC=3��AB=2��
��BC=
=
=
��
���߶�BC�ij���
��
��2����ͼ2����A��AH��x����H��AP��y����P����֤��ABH�ס�ACP��
��
=
��
=
��
=
��
��CP=
�� CP=

��OC=
��S=
•t•
=-
t2+
t
��t=
ʱ��S���=
��3���ٵ�0��t��3ʱ��
����E���A�غ�ʱ����CDEΪ���������Σ���ֱ��DE������A��
��
=2��
��t=
��
��B��
��0����
����ͼ3����3��t��
ʱ����CD=CE����A��AM��y�ᣬ
��֤��AMC�ס�DHC��
��
=
��
��
=
��t=��
��
��B��
��0����

����ͼ4����t��
ʱ����CEDΪ�۽ǣ���CE=DE��
��CF=BF��
��֤��OCF�ա�ABF��
��OC=AB��
�ࣨ
��2=��t-3��2+22
���t1=3 ����ȥ����t2=7.8��
��B ��7.8��0��
����ͼ5����t��0ʱ�������OF=
��
��CD=CEʱ��
��CB=CF��
��OB=OF
��
=-t��
���t=��
��
��B ��-
��0����
���ɢٿ�֪����B��
��0��ʱ��AF=AC������B�����˶�ʱ��AC������ͬʱAF��С��
�൱t��0ʱ������BC=BF�����Σ���������CD=DE�����Σ�
��CE=DE����CF=BF��
��֤��COF�ա�BAF��
��AB=OC��
�ࣨ
��2=��t-3��2+22��
���t1=3 ����ȥ����t2=7.8 ����ȥ����
�������������ڵ�Bʹ��DCEΪ���������Σ���ʱB������Ϊ��B1��
��0����B2��
��0����B3 ��7.8��0���� B4��-
��0����
 ��1���ߵ�A��3��2����
��1���ߵ�A��3��2������AC=3��AB=2��
��BC=
| AB2+AC2 |
| 22+32 |
| 13 |
���߶�BC�ij���
| 13 |
��2����ͼ2����A��AH��x����H��AP��y����P����֤��ABH�ס�ACP��
��
| AH |
| BH |
| AP |
| CP |
| 2 |
| 3-t |
| 3 |
| CP |
| 2 |
| t-3 |
| 3 |
| CP |
��CP=
| 9-3t |
| 2 |
| 3t-9 |
| 2 |

��OC=
| 13-3t |
| 2 |
��S=
| 1 |
| 2 |
| 13-3t |
| 2 |
| 3 |
| 4 |
| 13 |
| 4 |
��t=
| 13 |
| 6 |
| 169 |
| 48 |
��3���ٵ�0��t��3ʱ��
����E���A�غ�ʱ����CDEΪ���������Σ���ֱ��DE������A��
��
| 13-3t |
| 4 |

��t=
| 5 |
| 3 |
��B��
| 5 |
| 3 |
����ͼ3����3��t��
| 13 |
| 3 |
��֤��AMC�ס�DHC��
��
| HD |
| HC |
| AM |
| MC |
��
| ||
|
| 3 | ||
2-
|
��t=��
| 13 |
��B��
| 13 |

����ͼ4����t��
| 13 |
| 3 |
��CF=BF��
��֤��OCF�ա�ABF��
��OC=AB��
�ࣨ
| 13-3t |
| 2 |
���t1=3 ����ȥ����t2=7.8��
��B ��7.8��0��
����ͼ5����t��0ʱ�������OF=
| 3t-13 |
| t-3 |
��CD=CEʱ��
��CB=CF��

��OB=OF
��
| 3t-13 |
| t-3 |
���t=��
| 13 |
��B ��-
| 13 |
���ɢٿ�֪����B��
| 5 |
| 3 |
�൱t��0ʱ������BC=BF�����Σ���������CD=DE�����Σ�
��CE=DE����CF=BF��
��֤��COF�ա�BAF��
��AB=OC��
�ࣨ
| 13-3t |
| 2 |
���t1=3 ����ȥ����t2=7.8 ����ȥ����
�������������ڵ�Bʹ��DCEΪ���������Σ���ʱB������Ϊ��B1��
| 5 |
| 3 |
| 13 |
| 13 |
���������⿼���������ε��ۺ��⣮�漰��֪ʶ�У����������ε��ж������ʣ����ɶ�����������ͼ�����ʣ�����ֱ�������ε��ж������ʣ���һ��̽�����⣮

��ϰ��ϵ�д�
�����Ŀ
�и������л�Ϊ�෴�����ǣ�������
| A��32��-23 |
| B����-3��2��2��23����-3�� |
| C��-32�루-3��2 |
| D��-23�루-2��3 |
 ��ͼ����֪
��ͼ����֪ ��ͼ��ֱ��y=
��ͼ��ֱ��y=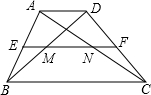 ��ͼ��������ABCD�У�AD��BC����λ��EF=2.6cm��EF�ֱ�AC��BD�ڵ�N��M����MN=0.8cm����AD��BC�ij���
��ͼ��������ABCD�У�AD��BC����λ��EF=2.6cm��EF�ֱ�AC��BD�ڵ�N��M����MN=0.8cm����AD��BC�ij��� �ڡ�ABC�У�BC=AC����C=90�㣬AC=7cm��AD�ǡ�BAC��ƽ���ߣ�DE��AB��E�����DEB���ܳ���
�ڡ�ABC�У�BC=AC����C=90�㣬AC=7cm��AD�ǡ�BAC��ƽ���ߣ�DE��AB��E�����DEB���ܳ���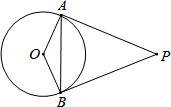 ��ͼ��PA��PB�ǡ�O�����ߣ�A��BΪ�е㣬��OAB=40�㣮���APB�Ķ���Ϊ
��ͼ��PA��PB�ǡ�O�����ߣ�A��BΪ�е㣬��OAB=40�㣮���APB�Ķ���Ϊ