题目内容
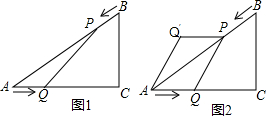 如图1,已知△ABC中,AB=10cm,AC=8cm,BC=6cm.如果点P由B出发沿BA方向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s.连接PQ,设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:
如图1,已知△ABC中,AB=10cm,AC=8cm,BC=6cm.如果点P由B出发沿BA方向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s.连接PQ,设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:(1)当t=
(2)如图2,把△AQP沿AP翻折,当t=
考点:相似形综合题
专题:
分析:(1)证△APQ∽△ABC,推出
=
,代入得出
=
,求出方程的解即可
(2)首先根据菱形的性质及相似三角形比例线段关系,求得PQ、QD和PD的长度;然后在Rt△PQD中,求得时间t的值.
| AP |
| AB |
| AQ |
| AC |
| 10-2t |
| 10 |
| 2t |
| 8 |
(2)首先根据菱形的性质及相似三角形比例线段关系,求得PQ、QD和PD的长度;然后在Rt△PQD中,求得时间t的值.
解答:解:(1)由题意知:BP=2t,AP=10-2t,AQ=2t,
∵PQ∥BC,
∴△APQ∽△ABC,
∴
=
,
∴
=
,
解得 t=
,
即当t为
s时,PQ∥BC.
(2)假设存在时刻t,使四边形AQPQ′为菱形,则有AQ=PQ=BP=2t.
∵△ABC中,AB=10cm,AC=8cm,BC=6cm,
∴AB2=AC2+BC2=100,
∴∠C=90°.
如图2所示,过P点作PD⊥AC于点D,则有PD∥BC,
∴
=
,即
,
解得:PD=6-
t,AD=8-
t,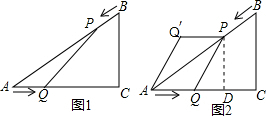
∴QD=AD-AQ=8-
t-2t=8-
t.
在Rt△PQD中,由勾股定理得:QD2+PD2=PQ2,
即(8-
t)2+(6-
t)2=(2t)2,
化简得:13t2-90t+125=0,
解得:t1=5,t2=
,
∵t=5s时,AQ=10cm>AC,不符合题意,舍去,
∴t=
.
故答案是:(1)
;(2)
.
∵PQ∥BC,
∴△APQ∽△ABC,
∴
| AP |
| AB |
| AQ |
| AC |
∴
| 10-2t |
| 10 |
| 2t |
| 8 |
解得 t=
| 20 |
| 9 |
即当t为
| 20 |
| 9 |
(2)假设存在时刻t,使四边形AQPQ′为菱形,则有AQ=PQ=BP=2t.
∵△ABC中,AB=10cm,AC=8cm,BC=6cm,
∴AB2=AC2+BC2=100,
∴∠C=90°.
如图2所示,过P点作PD⊥AC于点D,则有PD∥BC,
∴
| AD |
| AQ |
| AP |
| AB |
| 10-2t |
| 10 |
解得:PD=6-
| 6 |
| 5 |
| 8 |
| 5 |

∴QD=AD-AQ=8-
| 8 |
| 5 |
| 18 |
| 5 |
在Rt△PQD中,由勾股定理得:QD2+PD2=PQ2,
即(8-
| 18 |
| 5 |
| 6 |
| 5 |
化简得:13t2-90t+125=0,
解得:t1=5,t2=
| 25 |
| 13 |
∵t=5s时,AQ=10cm>AC,不符合题意,舍去,
∴t=
| 25 |
| 13 |
故答案是:(1)
| 20 |
| 9 |
| 25 |
| 13 |
点评:本题是非常典型的动点型综合题,全面考查了相似三角形线段比例关系、菱形的性质、勾股定理及其逆定理、一元一次方程的解法,涉及的考点众多,计算量偏大,有一定的难度.本题考查知识点非常全面,是一道测试学生综合能力的好题.

练习册系列答案
相关题目
下列图形中,轴对称图形的个数有( )

| A、4个 | B、3个 | C、2个 | D、1个 |
列各对数中互为相反数的是( )
| A、32与-23 |
| B、(-3×2)2与23×(-3) |
| C、-32与(-3)2 |
| D、-23与(-2)3 |
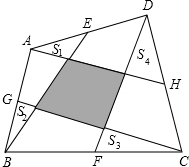 如图,E、G、F、H分别为任意四边形ABCD的边AD、AB、BC、CD的中点,图中阴影部分的面积为20平方厘米,求图中四个小三角形的面积和.
如图,E、G、F、H分别为任意四边形ABCD的边AD、AB、BC、CD的中点,图中阴影部分的面积为20平方厘米,求图中四个小三角形的面积和.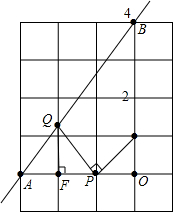 如图,直线y=
如图,直线y=