题目内容
已知,AD是△ABC中BC边上的中线,若AB=3,AC=7,则AD的取值范围是 .
考点:全等三角形的判定与性质,三角形三边关系
专题:
分析:作出图形,延长AD至E,使DE=AD,根据三角形中线的定义可得BD=CD,然后利用“边角边”证明△ABD和△ECD全等,根据全等三角形对应边相等可得CE=AB,再根据三角形的任意两边之和大于第三边,任意两边只差小于第三边求出AE,然后求解即可.
解答: 解:如图,延长AD至E,使DE=AD,
解:如图,延长AD至E,使DE=AD,
∵AD是△ABC中BC边上的中线,
∴BD=CD,
在△ABD和△ECD中,
,
∴△ABD≌△ECD(SAS),
∴CE=AB=3,
∵AC=7,
∴3+7=10,7-3=4,
∴4<AE<10,
∴2<AD<5.
故答案为:2<AD<5.
 解:如图,延长AD至E,使DE=AD,
解:如图,延长AD至E,使DE=AD,∵AD是△ABC中BC边上的中线,
∴BD=CD,
在△ABD和△ECD中,
|
∴△ABD≌△ECD(SAS),
∴CE=AB=3,
∵AC=7,
∴3+7=10,7-3=4,
∴4<AE<10,
∴2<AD<5.
故答案为:2<AD<5.
点评:本题考查了全等三角形的判定与性质,三角形的三边关系,“遇中线,加倍延”构造出全等三角形是解题的关键,作出图形更形象直观.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,CD是Rt△ABC斜边AB边上的高,AB=10cm,BC=8cm,则CD的长为( )
如图,CD是Rt△ABC斜边AB边上的高,AB=10cm,BC=8cm,则CD的长为( )| A、6cm | B、4.8cm |
| C、2.4cm | D、1.2cm |
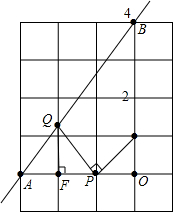 如图,直线y=
如图,直线y=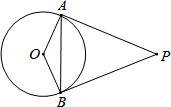 如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=40°.则∠APB的度数为
如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=40°.则∠APB的度数为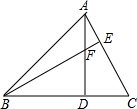 如图,△ABC中,AD⊥BC于D,BF=AC,FD=CD.求证:AC⊥BE.
如图,△ABC中,AD⊥BC于D,BF=AC,FD=CD.求证:AC⊥BE.