题目内容
12.如图1是一张邻边长为8和5的矩形纸片,将纸片依次按照如图的方式折叠,则图4中最厚处每层纸片的面积是1.
分析 先根据折叠得到FE=BE=4,EO=1,∠FEH=∠FEG=45°,再根据△EGH是等腰直角三角形,即可得到△EGH的面积=$\frac{1}{2}$GH×OE=1,进而得出图4中最厚处每层纸片的面积.
解答  解:如图4,由折叠可得,FE=BE=$\frac{1}{2}$BC=4,EO=5-4=1,∠FEH=$\frac{1}{2}$∠FEC=45°,∠FEG=$\frac{1}{2}$∠FEB=45°,
解:如图4,由折叠可得,FE=BE=$\frac{1}{2}$BC=4,EO=5-4=1,∠FEH=$\frac{1}{2}$∠FEC=45°,∠FEG=$\frac{1}{2}$∠FEB=45°,
∵EO⊥AD,
∴∠EGO=∠EHO=45°,
∴△EGH是等腰直角三角形,
∴GH=2OE=2,
∴△EGH的面积=$\frac{1}{2}$GH×OE=$\frac{1}{2}$×2×1=1,
由题可得,图3中最厚处有3层纸,
∴图4中,最厚处△GEH有6层纸,
∴图4中最厚处每层纸片的面积是1,
故答案为:1.
点评 本题主要考查了折叠问题,解题时注意:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
3.若不论x取何实数时,分式$\frac{a}{{x}^{2}-2x+a}$总有意义,则a的取值范围是( )
| A. | a≥1 | B. | a>1 | C. | a≤1 | D. | a<1 |
17.李老师新买了一辆小轿车,为了掌握车的耗油情况,在连续两次加油时做了如下工作:
(1)把油箱加满油;
(2)记录了两次加油时的累积里程(注:“累积里程”指汽车从出厂开始累积行驶的路程).以下是李老师连续两次加油时的记录:
则在这段时间内,该车每100千米平均耗油量为( )
(1)把油箱加满油;
(2)记录了两次加油时的累积里程(注:“累积里程”指汽车从出厂开始累积行驶的路程).以下是李老师连续两次加油时的记录:
| 加油时间 | 加油量(升) | 加油时的累计里程(千米) |
| 2017年3月18日 | 15 | 1200 |
| 2017年3月28日 | 30 | 1500 |
| A. | 15升 | B. | 10升 | C. | 7.5升 | D. | 5升 |
2.某工厂一月份产值为50万元,计划二、三月份总产值达到120万元,求二、三月份平均每月的增长率为多少?设二、三月份平均每月的增长率为x,根据题意,可列方程( )
| A. | 50(1+x)2=120 | B. | 50(1+x)+50(1+x)2=120 | ||
| C. | 50(1+x)3=120 | D. | 50+50(1+x)+50(1+x)2=120 |
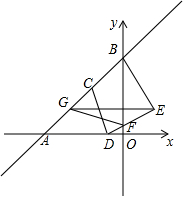 如图,在平面直角坐标系中,直线y=x+2分别交x轴、y轴于点A、B,设C为AB的中点,D是线段OA上的动点(OD<1),连结CD,将CD绕点D顺时针旋转90°至DE,交y轴于点F,过点E作x轴的平行线交AB于点G,连结FG,BE,则四边形BEFG面积的最小值为$\frac{7}{4}$.
如图,在平面直角坐标系中,直线y=x+2分别交x轴、y轴于点A、B,设C为AB的中点,D是线段OA上的动点(OD<1),连结CD,将CD绕点D顺时针旋转90°至DE,交y轴于点F,过点E作x轴的平行线交AB于点G,连结FG,BE,则四边形BEFG面积的最小值为$\frac{7}{4}$.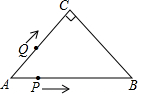 如图,在等腰Rt△ABC中,∠C=90°,AC=4$\sqrt{2}$cm,两个动点P,Q同时从点A出发,点P以1cm/s的速度沿AB运动,点Q以$\sqrt{2}$cm/s的速度沿折线AC-CB运动.当点P到达B时,P,Q停止运动,设运动时间为t秒.则当t=2$\sqrt{2}$或4+2$\sqrt{2}$秒时,△APQ的面积为4cm2.
如图,在等腰Rt△ABC中,∠C=90°,AC=4$\sqrt{2}$cm,两个动点P,Q同时从点A出发,点P以1cm/s的速度沿AB运动,点Q以$\sqrt{2}$cm/s的速度沿折线AC-CB运动.当点P到达B时,P,Q停止运动,设运动时间为t秒.则当t=2$\sqrt{2}$或4+2$\sqrt{2}$秒时,△APQ的面积为4cm2.