题目内容
1.化简求值(1)[(x-2y)2-4y2+2xy]÷2x,其中 x=1,y=-2.
(2)先化简,再求值:2(x-3)(x+2)-(3+a)(3-a),其中a=-2,x=1.
分析 (1)原式去括号合并得到最简结果,把x与y的值代入计算即可求出值;
(2)原式去括号合并得到最简结果,把a与x的值代入计算即可求出值.
解答 解:(1)[(x-2y)2-4y2+2xy]÷2x
=[x2-4xy+4y2-4y2+2xy]÷2x
=[x2-2xy]÷2x
=$\frac{1}{2}$x-y,
当x=1,y=-2时,原式=$\frac{1}{2}$+2=2$\frac{1}{2}$.
(2)2(x-3)(x+2)-(3+a)(3-a)
=2x2+4x-6x-12-9+a2
=2x2-2x-21+a2,
当a=-2,x=1时,原式=2-2-21+4=-17.
点评 考查了整式的加减-化简求值,给出整式中字母的值,求整式的值的问题,一般要先化简,再把给定字母的值代入计算,得出整式的值,不能把数值直接代入整式中计算.

练习册系列答案
相关题目
11.泰州某部门统计今年初三毕业的人数大约为3.14万人.那么该部门统计时精确到了( )
| A. | 百分位 | B. | 万位 | C. | 十分位 | D. | 百位 |
11.一次函数y=(m+3)x-5的函数值y随x的增大而减小,则m的取值是( )
| A. | m<3 | B. | m>3 | C. | m<-3 | D. | m>-3 |

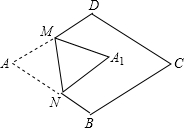 如图,在边长为2的菱形ABCD中,∠A=60°,M是边AD的中点,N是AB上一动点(不与A、B重合),将△AMN沿MN所在直线翻折得到△A1MN,连接A1C,画出点N从A到B的过程中A1的运动轨迹,A1C的最小值为$\sqrt{7}$-1.
如图,在边长为2的菱形ABCD中,∠A=60°,M是边AD的中点,N是AB上一动点(不与A、B重合),将△AMN沿MN所在直线翻折得到△A1MN,连接A1C,画出点N从A到B的过程中A1的运动轨迹,A1C的最小值为$\sqrt{7}$-1.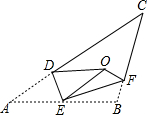 如图,将△ABC沿DE,EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=98°,则∠C的度数为=41°.
如图,将△ABC沿DE,EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=98°,则∠C的度数为=41°.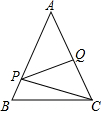 图中,P及Q分别为AB及AC上的点使得PQ为△APC的一条垂直平分线,若QC=6cm及△BCP的周长为21cm,求△ABC的周长.
图中,P及Q分别为AB及AC上的点使得PQ为△APC的一条垂直平分线,若QC=6cm及△BCP的周长为21cm,求△ABC的周长.