题目内容
7.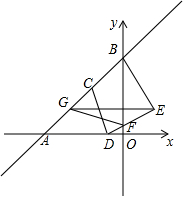 如图,在平面直角坐标系中,直线y=x+2分别交x轴、y轴于点A、B,设C为AB的中点,D是线段OA上的动点(OD<1),连结CD,将CD绕点D顺时针旋转90°至DE,交y轴于点F,过点E作x轴的平行线交AB于点G,连结FG,BE,则四边形BEFG面积的最小值为$\frac{7}{4}$.
如图,在平面直角坐标系中,直线y=x+2分别交x轴、y轴于点A、B,设C为AB的中点,D是线段OA上的动点(OD<1),连结CD,将CD绕点D顺时针旋转90°至DE,交y轴于点F,过点E作x轴的平行线交AB于点G,连结FG,BE,则四边形BEFG面积的最小值为$\frac{7}{4}$.
分析 先过C作CH⊥AO于H,过E作EM⊥AO于M,则∠CHD=∠DME=90°,根据旋转的性质,即可判定△CDH≌△DEM,进而得出CH=DM,DH=EM,再设OD=a,则DH=OH-a,进而得出OM=EM,即可得到平行四边形AOEG,进而得到GE=AO=2,根据S四边形BEFG=S△BFG+S△BFE=$\frac{1}{2}$BF×GE=$\frac{1}{2}$×BF×2=BF,BF=BO-FO=2-(a-a2)=a2-a+2,即可得出S四边形BEFG=(a-$\frac{1}{2}$)2+$\frac{7}{4}$,据此可得四边形BEFG面积的最小值.
解答  解:如图,过C作CH⊥AO于H,过E作EM⊥AO于M,则∠CHD=∠DME=90°,
解:如图,过C作CH⊥AO于H,过E作EM⊥AO于M,则∠CHD=∠DME=90°,
由旋转可得,∠CDE=90°,CD=ED,
∴∠HCD=∠MDE,
∴△CDH≌△DEM,
∴CH=DM,DH=EM,
设OD=a,则DH=OH-a,
∵C为AB的中点,CH∥BO,
∴OH=$\frac{1}{2}$AO=$\frac{1}{2}$×2=1,
∴DH=1-a=EM,
∵DM=CH=$\frac{1}{2}$BO=1,
∴OM=DM-DO=1-a,
∴OM=EM,
∵直线y=x+2分别交x轴、y轴于点A(-2,0)、B(0,2),
∴∠BAO=45°,
连接OE,则∠EOM=45°=∠GAO,
∴AG∥OE,
又∵EG∥OA,
∴四边形AOEG是平行四边形,
∴GE=AO=2,
∴S四边形BEFG=S△BFG+S△BFE=$\frac{1}{2}$BF×GE=$\frac{1}{2}$×BF×2=BF,
∵FO∥EM,
∴$\frac{OF}{ME}$=$\frac{DO}{DM}$,即$\frac{OF}{1-a}$=$\frac{a}{1}$,
∴OF=a-a2,
∴BF=BO-FO=2-(a-a2)=a2-a+2,
∴S四边形BEFG=a2-a+2=(a-$\frac{1}{2}$)2+$\frac{7}{4}$,
∵0<a<1,
∴当a=$\frac{1}{2}$时,四边形BEFG的面积最小值为$\frac{7}{4}$.
故答案为:$\frac{7}{4}$.
点评 本题考查了一次函数图象上点的坐标特征,平行四边形的判定以及全等三角形的判定与性质的综合应用,作辅助线构造全等三角形是解此题的关键.解题时注意运用割补法表示四边形BEFG的面积.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案| A. | 12×10-7 cm | B. | 1.2×10-7 cm | C. | 12×10-8 cm | D. | 1.2×10-8 cm |
| A. | $\left\{\begin{array}{l}k=0\\ b=0\end{array}\right.$ | B. | $\left\{\begin{array}{l}k=2\\ b=0\end{array}\right.$ | C. | $\left\{\begin{array}{l}k=3\\ b=1\end{array}\right.$ | D. | $\left\{\begin{array}{l}k=0\\ b=2\end{array}\right.$ |
| A. | 有最低点 | B. | 开口向上 | ||
| C. | 与y轴交点坐标是(0,3) | D. | 顶点坐标是(1,-2) |
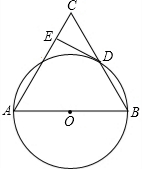 如图,在△ABC中,以AB为直径的⊙O与BC相交于点D,过点D作⊙O的切线交AC于点E.若⊙O的半径为5,∠CDE=20°,则$\widehat{BD}$的长为$\frac{10π}{9}$.
如图,在△ABC中,以AB为直径的⊙O与BC相交于点D,过点D作⊙O的切线交AC于点E.若⊙O的半径为5,∠CDE=20°,则$\widehat{BD}$的长为$\frac{10π}{9}$.
 图中的四边形均是矩形,根据图形,写出一个正确的等式:
图中的四边形均是矩形,根据图形,写出一个正确的等式: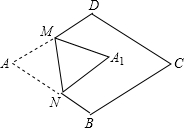 如图,在边长为2的菱形ABCD中,∠A=60°,M是边AD的中点,N是AB上一动点(不与A、B重合),将△AMN沿MN所在直线翻折得到△A1MN,连接A1C,画出点N从A到B的过程中A1的运动轨迹,A1C的最小值为$\sqrt{7}$-1.
如图,在边长为2的菱形ABCD中,∠A=60°,M是边AD的中点,N是AB上一动点(不与A、B重合),将△AMN沿MN所在直线翻折得到△A1MN,连接A1C,画出点N从A到B的过程中A1的运动轨迹,A1C的最小值为$\sqrt{7}$-1.