题目内容
13．某生态示范园，计划种植一批核桃，原计划总产量达36千克，为了满足市场需求，现决定改良核桃品种，改良后平均每亩产量是原计划的1.5倍，总产量比原计划增加了9万千克，种植亩数减少了20亩，则原计划和改良后平均每亩产量各为多少万千克？设原计划每亩平均产量x万千克，则改良后平均亩产量为1.5x万千克．根据题意列方程为（ ）| A． | $\frac{36+9}{1.5x}$-$\frac{36}{x}$=20 | B． | $\frac{36}{x}$-$\frac{36}{1.5x}$=20 | C． | $\frac{36}{x}$-$\frac{36+9}{1.5x}$=20 | D． | $\frac{36}{x}$+$\frac{36+9}{1.5x}$=20 |
分析 根据题意可得等量关系：原计划种植的亩数-改良后种植的亩数=20亩，根据等量关系列出方程即可．
解答 解：设原计划每亩平均产量x万千克，由题意得：
$\frac{36}{x}-\frac{36+9}{1.5x}$=20，
故选：C
点评 此题主要考查了由实际问题抽象出分式方程，关键是正确理解题意，找出题目中的等量关系．
练习册系列答案
相关题目
四边形ABCD中，点E、F、G、H分别为AB、BC、CD、DA边的中点，顺次连接各边中点得到的新四边形EFGH称为中点四边形．
5．二次函数的图象对称轴是y轴，顶点是原点，且过点（1，$\frac{1}{4}$），则此函数的关系式为（ ）
| A． | y=-$\frac{1}{4}$x2 | B． | y=$\frac{1}{4}$x2 | C． | y=-4x2 | D． | y=4x2 |
2．近年来，我国持续的大面积的雾霾天气让环境和健康问题成为焦点，为了调查学生对雾霾天气知识的了解程度，某校在学生中做了一次抽样调查，调查结果共分为四个等级：A．非常了解；B．比较了解；C．基本了解；D．不了解．根据调查统计结果，绘制了如图所示的不完整的三种统计图表．
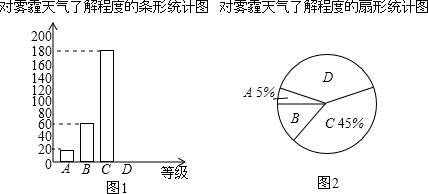
对雾霾所了解程度的统计表：
请结合统计图表，回答下列问题：
（1）本次参与调查的学生共有400人，n=35%；
（2）扇形统计图中D部分扇形所对应的圆心角是126度；
（3）请补全条形统计图；
（4）根据调查结果，学校准备开展关于雾霾的知识竞赛，某班要从“非常了解”程度的小明和小刚中选一人参加，现设计了如下游戏来确定，具体规则是：把四个完全相同的乒乓球标上数字1，2，3，4，然后放到一个不透明的袋中，一个人先从袋中随机摸出一个球，另一人再从剩下的三个球中随机摸出一个球．若摸出的两个球上的数字和为奇数，则小明去，否则小刚去．请用树状图或列表法说明这个游戏规则是否公平．
对雾霾所了解程度的统计表：
| 对雾霾的了解程度 | 百分比 |
| A．非常了解 | 5% |
| A．比较了解 | 15% |
| C．基本了解 | 45% |
| D．不了解 | n |
（1）本次参与调查的学生共有400人，n=35%；
（2）扇形统计图中D部分扇形所对应的圆心角是126度；
（3）请补全条形统计图；
（4）根据调查结果，学校准备开展关于雾霾的知识竞赛，某班要从“非常了解”程度的小明和小刚中选一人参加，现设计了如下游戏来确定，具体规则是：把四个完全相同的乒乓球标上数字1，2，3，4，然后放到一个不透明的袋中，一个人先从袋中随机摸出一个球，另一人再从剩下的三个球中随机摸出一个球．若摸出的两个球上的数字和为奇数，则小明去，否则小刚去．请用树状图或列表法说明这个游戏规则是否公平．