题目内容
10.定义:经过原点的抛物线y=a(x+m)2+n(a<0)与x轴交于点A,顶点为P,当△OAP为等腰直角三角形时,称抛物线y=a(x+m)2+n(a<0)为“正抛线”.下列关于正抛线的描述中,正确的是( )| A. | an=-1 | B. | m+n=0 | C. | m=n | D. | mn=a-2 |
分析 由抛物线y=a(x+m)2+n,得到P(-m,n),根据等腰直角三角形的性质得到m|=n,①当m>0时,m=n,②m<0时,-m=n,根据抛物线y=a(x+m)2+n过原点,即可得到结论.
解答 解:∵抛物线y=a(x+m)2+n,
∴P(-m,n),
∵△OAP为等腰直角三角形,
∴|m|=n,
①当m>0时,m=n,②m<0时,-m=n,
∵抛物线y=a(x+m)2+n过原点,
∴0=am2+n,∵m2=n2,∴0=an2+n,
∴an=-1,
故选A.
点评 本题考查了等腰直角三角形的性质,抛物线上点的坐标特征,熟练掌握等腰直角三角形的性质是解题的关键.

练习册系列答案
相关题目
5.在下列多项式的乘法中,不能用平方差公式计算的是( )
| A. | (c2-d2)(d2+c2) | B. | (x3-y3)(x3+y3) | C. | (-a-b)(a-b) | D. | (m-n)(-m+n) |
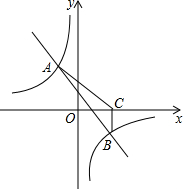 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(n,3),B(3,-1)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(n,3),B(3,-1)两点.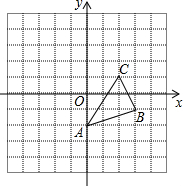 如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(0,-2),B(3,-1),C(2,1).平移△ABC使顶点C与原点O重合,得到△A′B′C′.
如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(0,-2),B(3,-1),C(2,1).平移△ABC使顶点C与原点O重合,得到△A′B′C′.