题目内容
2.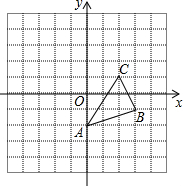 如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(0,-2),B(3,-1),C(2,1).平移△ABC使顶点C与原点O重合,得到△A′B′C′.
如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(0,-2),B(3,-1),C(2,1).平移△ABC使顶点C与原点O重合,得到△A′B′C′.(1)请在图中画出△ABC平移后的图形△A′B′C;直接写出点A′和B′的坐标:A′(-2,-3),B′(1,-2);
(2)点A′在第三象限,到x轴的距离为3,到y轴的距离为2;
(3)若P(a,b)为△ABC内一点,求平移后对应点P′的坐标.
分析 (1)根据图形平移的性质画出△A′B′C′,再由A′、B′在坐标系中的位置写出其坐标即可;
(2)根据A′所在的象限及坐标即可得出结论;
(3)根据两三角形对应点的位置写出平移的方向及距离,进而可得出结论.
解答  解:(1)如图所示,由图可知,A′(-2,-3),B′(1,-2).
解:(1)如图所示,由图可知,A′(-2,-3),B′(1,-2).
故答案为:(-2,-3),(1,-2);
(2)由图可知,点A′(-2,-3),
∴点A′在 三象限,到x轴的距离为3,到y轴的距离为2.
故答案为:三,3,2;
(3)∵由图可知,△ABC向左平移两个单位,再向下平移1个单位即可得到△A′B′C′,
∴P′(a-2,b-1).
点评 本题考查的是作图-平移变换,熟知图形平移后与原图形全等是解答此题的关键.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
12.已知A(x1,y1)是一次函数y=-x+b+1图象上一点,若x1<0,y1<0,则b的取值范围是( )
| A. | b<0 | B. | b>0 | C. | b>-1 | D. | b<-1 |
10.定义:经过原点的抛物线y=a(x+m)2+n(a<0)与x轴交于点A,顶点为P,当△OAP为等腰直角三角形时,称抛物线y=a(x+m)2+n(a<0)为“正抛线”.下列关于正抛线的描述中,正确的是( )
| A. | an=-1 | B. | m+n=0 | C. | m=n | D. | mn=a-2 |
11. 如图,△ABC内接于⊙O,AB=8,BC=10,AC=6,D是弧AB的中点,连接CD交AB于点E,则DE:CE等于( )
如图,△ABC内接于⊙O,AB=8,BC=10,AC=6,D是弧AB的中点,连接CD交AB于点E,则DE:CE等于( )
 如图,△ABC内接于⊙O,AB=8,BC=10,AC=6,D是弧AB的中点,连接CD交AB于点E,则DE:CE等于( )
如图,△ABC内接于⊙O,AB=8,BC=10,AC=6,D是弧AB的中点,连接CD交AB于点E,则DE:CE等于( )| A. | 2:5 | B. | 1:3 | C. | 2:7 | D. | 1:4 |
4.两条直线被第三条直线所截.下列叙述正确的是( )
| A. | 同位角一定不相等 | B. | 内错角的对顶角-定相等 | ||
| C. | 同位角的邻补角一定相等 | D. | 两对同旁内角的和一定大于180° |
 已知?ABCD的对角线交于点O,过O点的直线与AD交于点E,与BC交于点F,求证:OE=OF.
已知?ABCD的对角线交于点O,过O点的直线与AD交于点E,与BC交于点F,求证:OE=OF.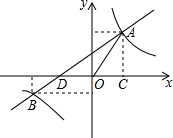 如图,在平面直角坐标系中,双曲线y=$\frac{m}{x}$与直线y=kx+b相交于A、B两点,过点A作AC⊥x轴于点C,其中AC=4,tan∠AOC=$\frac{4}{3}$且点B的坐标为(-6,n).
如图,在平面直角坐标系中,双曲线y=$\frac{m}{x}$与直线y=kx+b相交于A、B两点,过点A作AC⊥x轴于点C,其中AC=4,tan∠AOC=$\frac{4}{3}$且点B的坐标为(-6,n).