题目内容
15.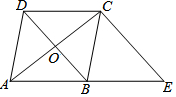 如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连结CE.
如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连结CE.(1)求证:BD=EC.
(2)当∠DAB=60°时,四边形BECD为菱形吗?请说明理由.
分析 (1)根据菱形的四条边的对边平行且相等可得AB=CD,AB∥CD,再求出四边形BECD是平行四边形,然后根据平行四边形的对边相等证明即可;
(2)只要证明DC=DB,即证明△DCB是等边三角形即可解决问题;
解答 (1)证明:四边形ABCD是菱形,
∴AB=CD,AB∥CD,
又∵BE=AB,
∴BE=CD,BE∥CD,
∴四边形BECD 是平行四边形,
∴BD=EC;
(2)解:结论:四边形BECD是菱形.
理由:∵四边形ABCD是菱形,
∴AD=AB,∵∠DAB=60°,
∴△ADB,△DCB是等边三角形,
∴DC=DB,
∵四边形BECD是平行四边形,
∴四边形BECD是菱形.
点评 本题考查了菱形的性质和判定,平行四边形的性质和判定,平行线的性质,熟记各图形的性质并准确识图是解题的关键.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
20.下列各数:3.14,$\sqrt{4}$,$\root{3}{9}$,-$\frac{22}{7}$,$\frac{\sqrt{5}}{2}$,π,其中无理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.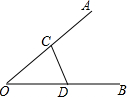 如图,在CD上找一点P,使得它到OA、OB的距离相等,则应找到( )
如图,在CD上找一点P,使得它到OA、OB的距离相等,则应找到( )
 如图,在CD上找一点P,使得它到OA、OB的距离相等,则应找到( )
如图,在CD上找一点P,使得它到OA、OB的距离相等,则应找到( )| A. | 线段CD的中点 | B. | CD与∠AOB平分线的交点 | ||
| C. | OC垂直平分线与CD的交点 | D. | OD垂直平分线与CD的交点 |
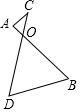 如图,AB=CD,AB与DC相交于点O,∠AOC=60°,请你利用平移的有关知识说明:AC+BD>AB.
如图,AB=CD,AB与DC相交于点O,∠AOC=60°,请你利用平移的有关知识说明:AC+BD>AB. 如图在8×8的正方形网格中,△ABC的顶点在边长为1的小正方形的顶点上.
如图在8×8的正方形网格中,△ABC的顶点在边长为1的小正方形的顶点上. 如图是“赵爽弦图”,其中△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,根据这个图形的面积关系,可以证明勾股定理.设AD=c,AE=a,DE=b,取c=10,a-b=2.
如图是“赵爽弦图”,其中△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,根据这个图形的面积关系,可以证明勾股定理.设AD=c,AE=a,DE=b,取c=10,a-b=2.