Question

18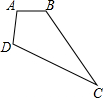．如果将四根木条首尾相连，在相连处用螺钉连接，就能构成一个平面图形．
（1）若固定三根木条AB，BC，AD不动，AB=AD=2cm，BC=5cm，如图，量得第四根木条CD=5cm，判断此时∠B与∠D是否相等，并说明理由．
（2）若固定二根木条AB、BC不动，AB=2cm，BC=5cm，量得木条CD=5cm，∠B=90°，写出木条AD的长度可能取得的一个值（直接写出一个即可）
（3）若固定一根木条AB不动，AB=2cm，量得木条CD=5cm，如果木条AD，BC的长度不变，当点D移到BA的延长线上时，点C也在BA的延长线上；当点C移到AB的延长线上时，点A、C、D能构成周长为30cm的三角形，求出木条AD，BC的长度．

Answer 1

分析 （1）相等．连接AC，根据SSS证明两个三角形全等即可．
（2）由勾股定理求出AC，再根据三角形三边的关系求出AD的取值范围．
（3）分两种情形①当点C在点D右侧时，②当点C在点D左侧时，分别列出方程组即可解决问题，注意最后理由三角形三边关系定理，检验是否符合题意．

解答 解：（1）相等．
理由：连接AC，
在△ACD和△ACB中，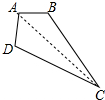
$\left\{\begin{array}{l}{AC=AC}\\{AD=AB}\\{CD=BC}\end{array}\right.$，
∴△ACD≌△ACB，
∴∠B=∠D．

（2）∵AB=2cm，BC=5cm，且∠B=90°，
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{2}^{2}+{5}^{2}}$=$\sqrt{29}$
根据三角形三边关系可知$\sqrt{29}$-5≤AD≤$\sqrt{29}$+5
所以AD可以为5cm．

（3）设AD=x，BC=y，
当点C在点D右侧时，$\left\{\begin{array}{l}{x+2=y+5}\\{x+（y+2）+5=30}\end{array}\right.$，解得$\left\{\begin{array}{l}{x=13}\\{y=10}\end{array}\right.$，
当点C在点D左侧时，点C在D左侧时，三边之和等于第四边是构不成四边形的，不合题意，
综上所述，AD=13cm，BC=10cm．

点评 本题考查全等三角形的判定和性质、二元一次方程组、三角形三边关系定理等知识，解题的关键是学会分类讨论，考虑问题要全面，属于中考常考题型．