题目内容
10.已知整式M=x2+5ax-x-1,整式M与整式N之差是3x2+4ax-x(1)求出整式N;
(2)若a是常数,且2M+N的值与x无关,求a的值.
分析 (1)根据题意,可得N=(x2+5ax-x-1)-(3x2+4ax-x),去括号合并即可;
(2)把M与N代入2M+N,去括号合并得到最简结果,由结果与x值无关,求出a的值即可.
解答 解:(1)N=(x2+5ax-x-1)-(3x2+4ax-x)
=x2+5ax-x-1-3x2-4ax+x
=-2x2+ax-1;
(2)∵M=x2+5ax-x-1,N=-2x2+ax-1,
∴2M+N=2(x2+5ax-x-1)+(-2x2+ax-1)
=2x2+10ax-2x-2-2x2+ax-1
=(11a-2)x-3,
由结果与x值无关,得到11a-2=0,
解得:a=$\frac{2}{11}$.
点评 此题考查了整式的加减,熟练掌握去括号与合并同类项法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10. 甲、乙两车从A城出发前往B城,在整个行程中,两车离开A城的距离y与t的对应关系如图所示,下列说法正确的说法有( )
甲、乙两车从A城出发前往B城,在整个行程中,两车离开A城的距离y与t的对应关系如图所示,下列说法正确的说法有( )
(1)A、B两城之间距离是300千米(2)甲车的速度是60千米/小时
(3)乙车出发4小时追上甲车(4)甲车出发2小时或3小时,两车相距20千米.
 甲、乙两车从A城出发前往B城,在整个行程中,两车离开A城的距离y与t的对应关系如图所示,下列说法正确的说法有( )
甲、乙两车从A城出发前往B城,在整个行程中,两车离开A城的距离y与t的对应关系如图所示,下列说法正确的说法有( )(1)A、B两城之间距离是300千米(2)甲车的速度是60千米/小时
(3)乙车出发4小时追上甲车(4)甲车出发2小时或3小时,两车相距20千米.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
11.已知关于x的分式方程$\frac{2x+m}{x-2}$=3的解是正数,则m可能的取值为( )
| A. | -7 | B. | -6 | C. | -5 | D. | -4 |
8.下列各数中,比-2小1的数是( )
| A. | -1 | B. | -3 | C. | 3 | D. | 1 |
15.圣诞节将至,小华决定购买一些贺卡,贺卡店有一则广告如图:
(1)如果小华只买15张,则购买贺卡共花去多少元钱?
(2)如果小华购买x张,请用含x的代数式表示小华所花的费用;
(3)如果小华此次购买共花去360元,请问购买贺卡可能多少张?
| 购买贺卡须知 (a)若购买20张以内(含20张),每张贺卡20元; (b)若购买20张以上,所购贺卡按照价格全部打七五折. |
(2)如果小华购买x张,请用含x的代数式表示小华所花的费用;
(3)如果小华此次购买共花去360元,请问购买贺卡可能多少张?
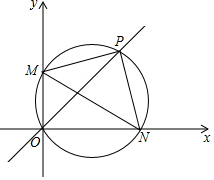 如图:M、N分别为直角坐标系x、y正半轴上两点,过M、N和原点O三点的圆和直线y=x交于点P,
如图:M、N分别为直角坐标系x、y正半轴上两点,过M、N和原点O三点的圆和直线y=x交于点P, 填空并完成以下推理:
填空并完成以下推理: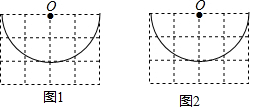 如图,在边长为1的正方形网格中画有一个圆心为O的半圆,请按要求准确作图.
如图,在边长为1的正方形网格中画有一个圆心为O的半圆,请按要求准确作图.